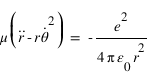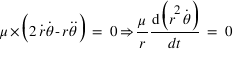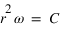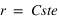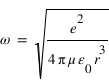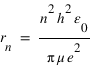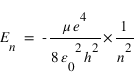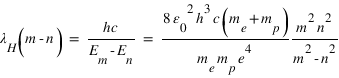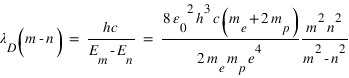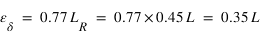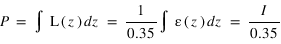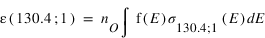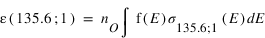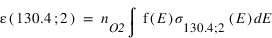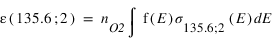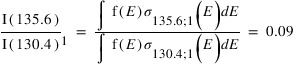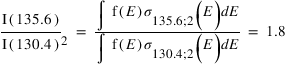Flux UV
Auteur: Jean-Yves Chaufray
- Décrire
- Introduction
- Emission Lyman-alpha de l'hydrogène atomique
- Dayglow et Nightglow
- Emissions aurorales
- Comprendre
- Structure Atomique de l'hydrogène
- Modèle de Bohr
- Coefficients d'Einstein
- Section efficace
- Diffusion résonante et diffusion fluorescente : Généralités
- Diffusion résonante et diffusion fluorescente : Exemple émission Lyman-alpha de l'hydrogène atomique
- Notation Spectroscopique
- Airglow : Généralités
- Exemple : La raie de l'oxygène à 297 nm
- Emission volumique
- Profils en altitude
- Emissions Aurorales: Généralités
- Emissions aurorales terrestres
- Emissions Aurorales des planètes géantes
- Autres emissions aurorales dans le système solaire
- Nightglow
- Exercices
- Exercice 1
- Exercice 2
- Exercice 3 : Emission UV sur Europe
- Mini Projet
- Airglow
- Aurores planétaires
-
Flux UV
Ce chapitre présente les principales émissions UV observées dans les hautes atmosphères des planètes. On décrit non seulement les émissions aurorales que l'on peut observer dans le visible depuis la surface de la Terre, mais aussi d'autres émissions plus ténues qui nous donnent des informations sur la composition, la dynamique et la variabilité des hautes atmosphères planétaires. Les différents processus à l'origine de ces émissions : interaction du rayonnement solaire avec l'atmosphère, précipitation de particules énergétiques, réactions chimiques, etc... sont décrits et illustrés par différents exemples dans le système solaire.
 Prérequis
Prérequis
- Mécanique du point
- Théorie cinétique des gaz
- Atomistique
Vous pouvez commencer le cours ici
Décrire
Auteur: Jean-Yves Chaufray
Introduction
Les luminescences atmosphériques sont des émissions lumineuses émises par les atmosphères planétaires. Elles sont produites par les espèces atomiques et moléculaires de l'atmosphère de la planète se trouvant dans des états de haute énergie (états excités) qui en redescendant vers un état de basse énergie émettent des photons.
Pour produire ce type d’émission il est donc nécessaire d’exciter les espèces atmosphériques le plus souvent par interaction avec un photon ou un électron. Les luminescences atmosphériques (appelées airglow) produites dans les hautes atmosphères planétaires (thermosphère/exosphère) peuvent généralement être classées en trois catégories :
Les émissions appelées « dayglow ». Le « dayglow » est l’émission de l’atmosphère de jour qui résulte de l’interaction du rayonnement solaire avec les gaz atmosphériques. Par définition, le « dayglow » inclus aussi les émissions produites par interactions entre les gaz atmosphériques et les photoélectrons, c’est à dire les électrons produits par la photoionisation de l’atmosphère de la planète.
Les émissions appelées « nightglow » qui sont les émissions luminescentes produites du côté nuit. Les réactions chimiluminescentes telles que les réactions de recombinaison entre deux atomes produisent des molécules dans des états excités à l'origine des émissions de type « nightglow » dans les hautes atmosphères planétaires.
Les émissions aurorales qui peuvent être définies comme les émissions résultant de l’impact de particules énergétiques autres que les photoélectrons, comme par exemple lors de précipitations d’électrons énergétiques de la magnétosphère terrestre dans les régions polaires.
L’énergie perdue par l’atmosphère sous forme de luminescences atmosphériques ne représente qu’une fraction minime de l’énergie absorbée par l’atmosphère. Une partie de l’énergie absorbée est aussi transformée en énergie thermique (chauffage) et énergie cinétique (dynamique).
Emission Lyman-alpha de l'hydrogène atomique
Avant de voir en détails les principaux mécanismes d ’émissions, voici quelques exemples d’émissions observées dans l’UV et le visible sur différents objets du système solaire
 Emission Lyman-alpha de l'hydrogène atomique
Emission Lyman-alpha de l'hydrogène atomique
A cause de la gravité, les espèces légères, comme l’hydrogène atomique deviennent les principaux composants des très hautes atmosphères (exosphère) des planètes. L’hydrogène atomique peut diffuser de façon efficace le rayonnement solaire et former une couronne lumineuse en UV autour de la planète. Cette émission a été observée pour la première fois autour de la Terre à la fin des années 50. Elle avait d’abord été interprétée comme la diffusion du rayonnement solaire par les atomes d’hydrogène du milieu interplanétaire avant d’être interprétée comme l’émission d’atomes d’hydrogène liée gravitationnellement à la Terre et formant autour d’elle une « géocouronne ».
Des couronnes similaires ont été mises en évidence autour de toutes les planètes du système solaire (Mercure, Vénus, Mars, Jupiter, Saturne, Uranus, Neptune) , de certains satellites (Titan, ...)et des comètes. Des tentatives d’observations par la sonde Rosetta n’ont pas permis de mettre en évidence une « couronne » d’hydrogène autour des astéroïdes Lutetia et Steins.
La couronne d’une planète pouvant s’étendre sur plusieurs rayons planétaires, cette émission peut être observée côté jour et côté nuit. D’autres espèces comme l’hélium ou l’oxygène atomique conduisent à des émissions exosphériques observables en UV.
Le milieu interplanétaire composé essentiellement d’hydrogène atomique produit lui aussi une émission par diffusion du rayonnement solaire et la première carte complète de l’émission de l’hydrogène interplanétaire vue depuis la Terre a été effectuée par le satellite OGO-5.
Dayglow et Nightglow
Emissions dayglow des planètes telluriques
L’atmosphère de la Terre est composée essentiellement de N2 et de O2. Les principales émissions UV observées dans la thermosphère de la Terre côté jour sont des émissions produites par O, O+, N+, N2 et NO.
Sur Mars et Vénus, l’atmosphère est essentiellement composée de CO2 et les principales émissions observées en UV côté jour sont les mêmes et sont produites par CO, CO2+ et O.
Ces émissions résultent de différent processus induit par le rayonnement solaire qui seront décrites en détails dans la partie Comprendre.
Emissions nightglow des planètes telluriques
Sur Mars et Vénus et la Terre, des bandes d’émissions UV de NO sont visibles du côté nuit, à ces bande d’émissions, s’ajoutent des bandes d’émissions de O2 sur la Terre.
Ces émissions sont produites par des réactions chimiques de recombinaison (chimiluminescence) entre des atomes d’azote et des atomes d’oxygène. Ces atomes sont produits par la photodissociation de CO2 et N2 du côté et transporté par les vents vers la nuit où ils peuvent se recombiner.
Emissions aurorales
Généralités
Les émissions aurorales sont des émissions produites par interaction entre des particules très énergétiques (le plus souvent des électrons) provenant de l’environnement spatial voisin de la planète (magnétosphère par exemple) et les composés de l’atmosphère de la planète.
Les émissions aurorales peuvent être observées dans toutes les gammes spectrales du spectre électromagnétique : des rayons gammas au émissions radios. Dans ce cours on se limitera aux émissions UV-visible.
L’excitation peut être directement produite par la particule énergétique incidente ou produite par une cascade de collisions dans l’atmosphère.
Des émissions aurorales ont été observées sur la Terre et les quatre planètes géantes du système solaire. Des émissions aurorales ont aussi été observées sur Vénus, Mars et sur certains satellites galiléens (Ganymède, Io, Europe).
Emissions aurorales terrestres
Les principales émissions aurorales visibles observées sur Terre sont les raies vertes et rouges de l’oxygène atomique. Les observations des émissions aurorales en UV montrent un spectre riche en raies principalement associées à N, O, N+, O+, N2. Ces émissions sont observées aux hautes latitudes, au voisinage des pôles magnétiques, où les électrons accélérés dans la magnétosphère de la Terre peuvent précipiter dans l’atmosphère le long des lignes de champs magnétique.
Emissions aurorales des planètes géantes
Les émissions aurorales observées sur les planètes géantes sont aussi principalement produites par des précipitations d’électrons magnétosphériques près des pôles magnétiques. Les émissions UV sont dominées par les émissions de H et H2. La morphologie des émissions aurorales sur Jupiter et Saturne montrent différentes structures qui seront présentées dans la suite de ce cours.
Les émissions aurorales UV des géantes glacées Neptune et Uranus ont été observées pour la première fois par la sonde Voyager 2.
Comprendre
Auteur: Jean-Yves Chaufray
Structure Atomique de l'hydrogène
L'atome est le constituant de base de la matière; il est formé d'un noyau chargé positivement et d'un nuage d'électrons chargé négativement. Le noyau contient A nucléons, dont Z protons chargé positivement et (A-Z) neutrons de charge nulle. Un atome est électriquement neutre et contient donc Z protons et Z électrons. Des atomes ayant un nombre Z identique mais un nombre A différent sont appelés isotopes. Par exemple, l'atome de deutérium composé de 1 proton, 1 neutron et 1 électron (Z=1, A=2) est un isotope de l'hydrogène composé de 1 proton et 1 électron (Z=1, A=1). La science qui étudie la structure interne des atomes s'appelle l'atomistique.
La dispersion de la lumière par un gaz atomique présente une structure sous forme de raies. Chaque élément a un spectre de raies caractéristiques, par exemple l'hydrogène et le deutérium possèdent plusieurs séries de raies portant le nom des scientifiques qui les ont observées pour la première fois. La série des raies de Lyman dans l'ultraviolet a été observée pour la première fois par Théodore Lyman en 1906. Johann Balmer a découvert quatre raies de la série de Balmer en 1885 dans le visible.
Johannes Rydberg et Walter Ritz montrèrent que les longueurs d'onde des différentes séries pouvaient être décrites par la formule de Rydberg-Ritz:
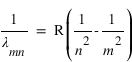 R est la constante de Rydberg, m et n sont deux nombres entiers. La structure en raies des spectres d'émission des atomes et la présence de nombre entiers dans l'équation de Rydberg suggère une quantification de l'énergie des électrons dans le nuage atomique, on parle de niveaux d'énergie. Les valeurs de l'énergie sont quantifiées par un nombre entier n et données par
R est la constante de Rydberg, m et n sont deux nombres entiers. La structure en raies des spectres d'émission des atomes et la présence de nombre entiers dans l'équation de Rydberg suggère une quantification de l'énergie des électrons dans le nuage atomique, on parle de niveaux d'énergie. Les valeurs de l'énergie sont quantifiées par un nombre entier n et données par
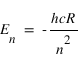 ou h est la constante de Planck et c la vitesse de la lumière dans le vide. Une raie d'émission résulte d'une transition d'un électron du niveau m vers le niveau n (m>n).
Cette quantification de l'énergie d'un atome ne peut s'expliquer par la physique classique. Bohr présentera un premier modèle théorique permettant de démontrer la formule de Rydberg-Ritz en 1913, mais c'est la physique quantique développée dans les années 1920 par Schrodinger et Heisenberg, puis la théorie des champs développée par Dirac qui permettront non seulement de retrouver la formule de Rydberg-Ritz mais aussi d'expliquer toutes les observations de la structure de l'hydrogène.
L'étude des émissions spectroscopiques est à la base de l'astrophysique.
ou h est la constante de Planck et c la vitesse de la lumière dans le vide. Une raie d'émission résulte d'une transition d'un électron du niveau m vers le niveau n (m>n).
Cette quantification de l'énergie d'un atome ne peut s'expliquer par la physique classique. Bohr présentera un premier modèle théorique permettant de démontrer la formule de Rydberg-Ritz en 1913, mais c'est la physique quantique développée dans les années 1920 par Schrodinger et Heisenberg, puis la théorie des champs développée par Dirac qui permettront non seulement de retrouver la formule de Rydberg-Ritz mais aussi d'expliquer toutes les observations de la structure de l'hydrogène.
L'étude des émissions spectroscopiques est à la base de l'astrophysique.
Modèle de Bohr
Coefficients d'Einstein
Les processus d'émission et d'absorption peuvent être décrits de façon probabiliste à l'aide de coefficients appelés coefficients d'Einstein. Ces coefficients ont été introduits par Einstein en 1917, avant le développement de la théorie quantique. Trois processus possibles ont été postulés par Einstein :
-
L'émission spontanée : Un atome passe spontanémént d'un état excité 2 vers un état de plus basse énergie 1. Ce processus est caractérisé par un coefficient A21 définit par:
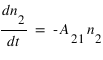
où n2 est le nombre d'atomes dans l'état excité 2
-
L'absorption : Un atome passe d'un état 1 vers un état de plus haute énergie 2 par absorption d'un photon de fréquence ν =(E2-E1)/h. Ce processus dépend de la densité volumique d'énergie rayonné à la fréquence ν : u(ν) et se caractérise par un coefficient B12 définit par
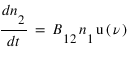
-
L'émission stimulée. Comme dans le cas de l'émission spontanée, un atome passe d'un état excité 2 vers un état de plus bassé énergie 1, mais cette fois cette émission est stimulée par un rayonnement incident à la fréquence de la transition. Comme l'absorption, ce processus dépend de la densité volumique d'énergie rayonné à la fréquence ν : u(ν) . Il se caractérise par un coefficient B21 définit par :
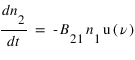
Nous ne décrirons pas plus en détails ce processus d'émissions stimulée, qui représente un apport majeur d'Einstein et sera à l'origine du développement des lasers.
L'équilibre thermodynamique entre émission spontanée, stimulée et absorption permet de retrouver la loi du corps noir. C'est d'ailleurs pour expliquer la loi de rayonnement du corps noir que Einstein a été amené à postuler le mécanisme d'émission stimulée.
Si un atome dans un état excité 2 peut se désexciter vers plusieurs niveaux inférieurs 1a, 1b, 1c, ..., l'inverse de la somme des coefficients d'émission spontanée d'Einstein sur toutes les transitions 1x représente la durée de vie de l'état excité 2:
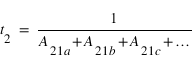
Section efficace
Considérons un flux de particules (par exemple un flux de photons ou un flux d'électron), Φ∞ arrivant au sommet d'une atmosphère planétaire. On suppose que les particules décrivent des trajectoires rectilignes le long desquelles elles peuvent interagir avec les espèces atmosphériques. Pour simplifier on supposera que l'atmosphère n'est composée que d'une celle espèce A.
Le flux de particules dΦint qui interagit avec l'atmosphère le long d'un segment élémentaire ds de la trajectoire est proportionnelle à la densité de A, au flux incident et à la longeur ds du segment.
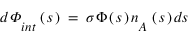
Section Efficace
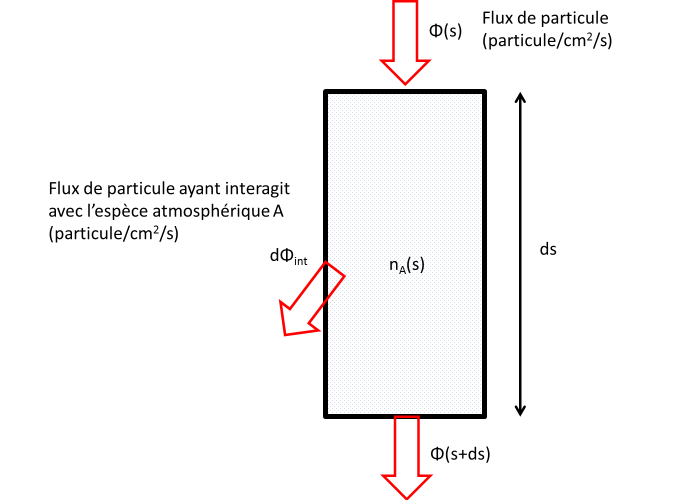
La constante de proportionnalité σ à la dimension d'une surface. On l'appelle section efficace d'interaction entre l'espèce incidente et l'espèce A. Elle dépend de l'énergie des particules incidentes (donc de la longeur d'onde pour un photon). Cette section efficace mesure l'efficacité d'une interaction donnée entre A et les électrons ou les photons incidents.
Diffusion résonante et diffusion fluorescente : Généralités
La diffusion résonante d'un photon par un atome peut être vu comme la succession d'une transition atomique de l'état électronique fondamental (n=1) vers un état excité (m) par absorption d'un photon puis la désexcitation vers le niveau fondamental associé à l'émission d'un photon. Si la desexcitation se fait vers un ou plusieurs états excités intermédiaires (p avec n <p<m) avant d'atteindre l'état fondamental, on parle de diffusion fluorescente. Dans le dernier cas les photons émis ont des longueurs d'onde supérieures à la longueur d'onde du photon incident.
Diffusion résonante et diffusion fluorescente : Exemple émission Lyman-alpha de l'hydrogène atomique
L'hydrogène est l'espèce neutre majoritaire dans l'Univers. Toutes les planètes du système solaire contiennent de l'hydrogène sous forme atomique qui domine à hautes altitudes. Sur les planètes telluriques comme Vénus, la Terre et Mars, cet hydrogène est produit par la dissociation de la vapeur d'eau atmosphérique. A haute altitude, cet hydrogène peut diffuser le rayonnement solaire à 121.6 nm (UV) dans toutes les directions. L'intensité du flux diffusé est d'autant plus intense que le rayonnement solaire est intense, donc que la planète est proche du Soleil.
On défiinit le facteur d'excitation gexc comme le nombre moyen de diffusions par seconde et par atome d'hydrogène. Lorsque le milieu est assez dilué, cette fréquence de diffusion est donnée par:
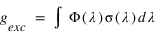
ou Φ(λ) est le flux solaire à la longueur d'onde λ (en photons/nm/s/m2) et σ(λ) la section efficace de diffusion d'un atome d'hydrogène à la longueur d'one λ (en m2). Le profil spectral de la section efficace n'est pas une fonction infiniment fine à 121.6 nm. Elle possède une certaine largeur spectrale qui peut résulter de différents mécanismes.
- Elargissement naturel : L'inégalité d'Heisenberg relie l'incertitude sur l'énergie d'un photon émis lors d'une transition d'un état excité vers un état de plus basse énergie et la durée de vie de cet état excité. La mesure de la longeur d'onde d'un photon émis lors d'une transition n'est donc jamais exactement la même.
- Elargissement par effet Doppler : La longueur d'onde d'un photon solaire est décalé vers le rouge ou vers le bleu selon que l'atome d'hydrogène s'éloigne ou s'approche du Soleil. Tous les atomes d'hydrogène n'ont pas exactement la même vitesse. La distribution des vitesses, dans un milieu à l'équilibre thermodynamique local a une forme gaussienne. La largeur de cette distribution dépend de la température du milieu. Elle est d'autant plus large que la température est élevée.
- Elargissment par collisions: Les collisions peuvent modifier légèrement l'énergie des états excités et donc la longueur d'onde d'une transition.
Si l'on néglige l'élargissement naturel de la raie et l'élargissement par collisions. La section efficace suit un profil et gaussien et peut s'écrire sous la forme:
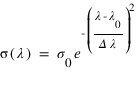
ou σ0 est la section efficace au centre du profil, Δλ est la largeur Doppler du profil.
Si par ailleurs on suppose que le flux solaire à un profil spectral "plat" : un profil spectral constant avec la longueur d'onde (Φ(λ) = Φ0) au voisinage de 121.6 nm, le facteur d'excitation se calcule facilement et l'on obtient:
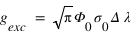
Le nombre de photons diffusés par unité de volume et de temps s'appelle le taux d'émission volumique, il est simplement donné par le produit entre le facteur d'excitation et la densité d'hydrogène (atome/cm3).
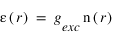
Ce taux volumique d'émission n'est en général pas mesurable directement, un instrument optique mesure seulement son intégrale sur une ligne de visée. On appelle intensité cette intégrale :
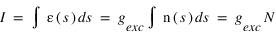
s est la coordonée curviligne le long de la ligne de visée. L'intégrale de la densité sur la ligne de visée, notée N est la colonne densité le long de la ligne de visée, elle s'exprime en général en atome/cm3. Cette grandeur est utile car c'est elle qui peut être directement déterminée par le rapport entre l'intensité mesurée et le facteur d'excitation généralement connu. L'intensité peut s'exprimer en photons/cm2/s. On préfère souvent utilisé une autre unité appelé Rayleigh, noté R définit par
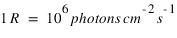

La diffusion résonante est le principal mécanisme produisant l'émission Lyman-alpha observée en UV autour des planètes. De nombreuses autres émissions sont produites par ce mécanisme comme par exemple la raie de l'oxygène atomique à 130.4 nm, la raie de l'ion O+ à 83.4 nm ou la raie du carbone atomique C à 156.5 nm. Dans le domaine visible on peut aussi citer la raie du sodium à 589 nm, dont la section efficace est suffisamment grande pour que cette émission soit observée dans des milieux extrêmement ténus comme les "atmosphères" de la Lune ou de Mercure.
Notation Spectroscopique
Avant de voir les autres processus d'émissions, voici quelques rappels et éléments de notation spectroscopique qui seront utilisés dans la suite pour nommer les etats excités des atomes polyatomiques.
Dans le cadre du modèle de Slater, la fonction d'onde polyelectronique peut s'écrire comme le produit de fonctions d'onde monoélectronique, appelée orbitale atomique qui dépend de 3 nombres quantiques :
- Le nombre quantique principal n on parle de "couche n"
- Le nombre quantique secondaire l : 0 ≤ l ≤ n-1, si l =0, on parle de "sous couche s", si l = 1 "sous couche p", si l =2 "sous couche d"...
- Le nombre quantique magnétique ml :-l ≤ ml ≤ l
Pour une valeur n+l donnée, il y a 2l+1 orbitales atomiques de même énergie chacune correspondant à un nombre quantique ml différent.
Pour chaque orbitale atomique, on peut définir 2 spin-orbitales, caractérisées par un nombre quantique de spins ms = ± 1/2 différents.
D'après le principe d'exclusion de Pauli, on a au maximum deux électrons (de nombres quantiques de spin ms opposés) par orbitale atomique. Deux électrons ne peuvent pas être décrit par une même spin-orbitale (n,l,ml,ms).
La règle de Klechkowsky permet de d'ordonner les orbitales atomiques en fonction de leur énergie :
- L'énergie des orbitales atomiques est une fonction croissante du nombre n+l
- Pour une valeur n+l donnée, l'énergie de l'orbitale atomique augmente avec n
Une fois la règle de Klechkowsky vérifiée, La règle de Hund permet de déterminer les spins des différents électrons de la dernière couche électronique :
L'état minimum d'énergie est celui pour lequel le spin total est maximum.
L'état fondamental d'un atome est son état de plus basse énergie. La répartition des électrons dans les différentes orbitales atomiques de l'atome à l'état fondamental doit donc minimiser l'énergie du système. La construction de la configuration électronique fondamentale d'un atome s'effectue à l'aide des règles de Klechkowsky, de Hund et du principe d'exclusion de Pauli.
La configuration électronique du carbone (6 électrons) est 1s22s22p2
La configuration électronique de l'oxygène (8 électrons) est 1s22s22p4
Les électrons de valence, sont les électrons de la dernière couche n remplie, l'atome de carbone possède 4 électrons de valence, l'atome d'oxygène possède 6 électrons de valence.
Un état atomique pour un atome polyélectronique peut aussi être noté sous la forme 2S+1L ou S est la somme des spins des différents électrons et 2S+1 est appelée la multiplicité de spin. Le symbol L est définit par le nombre quantique orbital total des électrons, par analogie avec la notation des orbitales atomiques. Ainsi, si le nombre quantique orbital total L = 0, le symbole utilisé est S, si L =1 le symbole est P, si L=2, le symbole est D etc...
Pour l'atome d'oxygène de configuration électronique 1s22s22p4 Les électrons des couches s (l=0) ont des nombres quantiques orbitaux nuls, par ailleurs ces couches sont entièrement remplies, leur contribution au spin total S est donc nulle. Seuls les 4 derniers électrons vont contribuer aux nombres quantiques S et L. La couche p est définit par un nombre quantique l =1, elle est composée de trois sous couches ml = -1, 0 et 1. La règle de Hund (maximisation de S, et pour un spin S donné maximisation de L) et le principe d'exclusion de Pauli (les électrons ne peuvent pas se trouver dans le même état quantique (n,l,ml,ms) permet de remplir les trois sous couches:
Le nombre L total vaut donc L= 2x(1)+0-1=1, le symbol du niveau fondamental de l'atome d'oxygène est donc P.
Le nombre S total vaut S = +1/2 -1/2 +1/2+1/2 = 1 donc 2S+1=3, la notation du niveau fondamental de l'atome d'oxygène est donc 3P.
Airglow : Généralités
Illustration
La diffusion résonante n'est pas le seul mécanisme à l'origine de l'airglow planétaire, dans les pages suivantes nous allons voir d'autres exemples de mécanismes de façon plus succinte. Les différents processus possibles sont représentés de façon schématique sur cette figure.
Mécanismes d'émissions
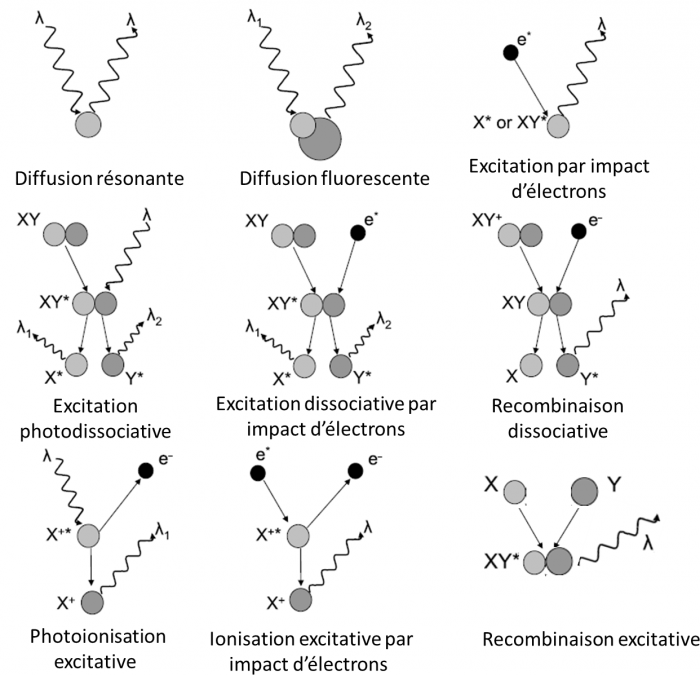
Principaux mécanismes à l'origine de l'airglow planétaire
Crédit :
adapté de Leblanc et al. JGR, 111, E09S11
La diffusion résonante a été décrite dans la section précédente. Lors d'une diffusion fluorescente, l'atome excité par le rayonnement solaire ne revient pas directement dans son état fondamental mais passe par un état électronique intermédiaire. Le photon diffusé à donc une longeur d'onde supérieure à la longueur d'onde du photon incident. Ce type d'émission à été observée sur Jupiter pour la molécule H2.
L'excitation par impact d'électrons produit des émissions pour des transitions dites "interdites" c'est à dire des transitions qui ne peuvent pas être produites par des photons solaires. La raie de l'oxygène à 135.6 nm est un exemple de raie interdite observée dans les atmosphères de Vénus, Mars et la Terre. Les électrons peuvent être des électrons produit par ionisation de l'atmosphère neutre par le rayonnement UV solaire ("photoélectrons"), dans ce cas l'émission est appelée "dayglow" ou des électrons énergétiques précipitant dans l'atmosphère, dans ce cas l'émission est appelée émission aurorale.
L'excitation dissociative résulte de la dissociation d'une molécule par interaction avec un photon solaire ou un électron dont au moins un des produits de la dissociation se trouve dans un état excité. Sur Terre, la dissociation de O2 peut produit un atome d'oxygène dans un état excité noté 1S qui en se relaxant vers le niveau fondamental (3P) produit un rayonnement à 297 nm. Cette émission est aussi observée sur Mars, mais elle est essentiellement due à la dissociation de CO2 et non pas O2 qui est le principal constituant atmosphérique. L'état 1S peut se désexciter vers un niveau intermédiaire: le niveau 1D avant le niveau fondamental. Les transitions 1S → 1D et 1D → 3P émettent un rayonnement dans le visible correspondant aux raies rouge (630 nm) et verte (557.7 nm) de l'oxygène caractéristique des émissions aurorales terrestres.
Récemment, la sonde Rosetta a observé des raies d'émissions produites par la dissociation de la vapeur d'eau cométaire suite aux impacts avec des électrons énergétiques autour de la comète 67P Churyumov-Gerasimenko.
La recombinaison dissociative résulte de l'interaction d'un ion moléculaire avec un électron. La capture de l'électron conduit à la formation d'un intermédiaire réactionnel instable qui se dissocie. Un ou plusieurs produits de la dissociation peuvent se trouver dans un état excité et produire un rayonnement. La recombinaison des ions O2+ peut conduire à la formation d'atomes d'oxygène dans les états 1D, 1D ou 3P conduisant à des émissions à 297, 557 et 630 nm.
L'ionisation excitative par interaction d'une espèce neutre avec un photon ou un électron est la source principale de l'émission de CO2+ à 289 nm observée sur Mars et Vénus par ionisation de CO2.
Exemple : La raie de l'oxygène à 297 nm
Le plus souvent une émission est produite par plusieurs mécanismes dont l'importance peut varier en fonction de l'altitude. A titre d'exemple on va étudier plus en détails la raie de l'oxygène à 297 nm observée dans le dayglow martien.
Schéma d'émissions de l'atome d'oxygène
Les principales voies d'excitation et de désexcitation de l'oxxygène atomique sont représentées sur cette figure. La raie à 297 nm de l'oxygène correspond à la transition 1S → 3P.
Représentation schématique des émissions de l'oxygène atomique
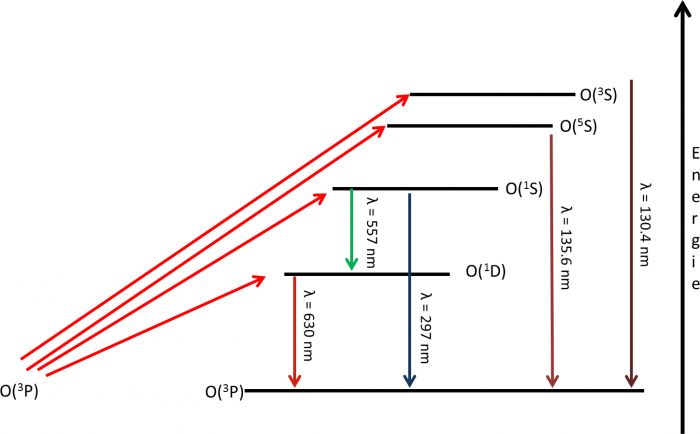
L'oxygène atomique dans l'état 1S peut être produit par les mécanismes d'excitation suivants :
-
Excitation photodissociative de CO2
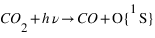
-
Excitation dissociative par impact d'électron sur CO2
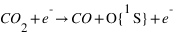
-
Recombinaison dissociative des ions O2+
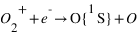
-
Excitation par impact d'électrons sur O
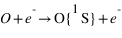
Emission volumique
Pour chaque processus, on définit le taux de production de O dans l'état excité 1S, c'est à dire le nombre d'atomes d'oxygène produit dans l'état 1S par unité de volume et par unité de temps. Pour les deux premiers processus décrit à la page précédente, ce taux de production est proportionnel à la densité de CO2. Pour le troisième processus il est proportionnel à la densité de O2+ et pour le dernier processus il est proportionnel à la densité de O.
Le taux de production Q1 du premier processus est donné par:
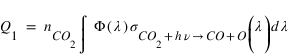
Φ(λ) étant le flux solaire à la longueur d'onde λ et σCO2+hν → CO+O(1S) ) la section efficace du processus considéré pour la longueur d’onde λ.
Le taux de production Q2 du second processus est donné par
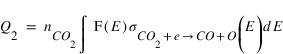
F(E) étant le flux de photoélectrons d'énegie E et σCO2+e→CO +O(E) la section efficace de ce processus pour un életron d'énergie E
Le taux de production Q3 du troisième processus a une forme similaire à celle du processus 2
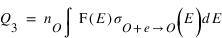
Le taux de production du Q4 du quatrième processus peut s'écrire sous une forme identique à Q2 et Q3. Cependant, contrairement aux processus 2 et 3 qui nécessitent des électrons avec des énergies suffisante pour dissocier CO2 ou exciter O. La recombinaison dissociative se fait principalement avec des électrons de basse énergie dont la distribution en énergie est bien décrite par une distribution maxwellienne. L'intégration peut alors être remplacée par une fonction ne dépendant que de la densité et de la température des électrons. Le terme Q4 peut alors s'écrire sous la forme
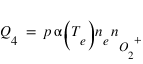
Le coefficient α est appelé coefficient de réaction et contient tout l'information de nature cinétique. Il dépend de la température des électrons, p est un nombre compris entre 0 et 1 qui représente la probabilité que l'état excité 1S soit produit par la réaction (p ~ 4%).
L'atome dans l'état excité 1S produit par un des quatre mécanismes ci-dessus peut se désexciter vers l'état 1D ou l'état fondamental 3P. Seule la desexcitation vers l'état 3P conduit à l'émission d'un photon de longeur d'onde 297 nm. Les proportions de desexcitation de 1S vers 3P et 1S vers 1D sont directement proportionnel aux coefficients d'Einstein des transitions notés A297 et A557.
L'émission volumique totale à 297 nm est donc donnée par
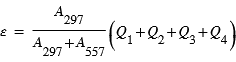
Dans ce calcul, on a négligé les processus de désexcitation par collisions (quenching). Ce terme peut être pris en compte en ajourant sa fréquence au dénominateur
Profils en altitude
La figure représente un exemple de modélisation du taux d'émission volumique du rayonnement à 297 nm décrits auparavant ainsi que leur somme ε.
Modélisation de la raie à 297 nm de l'oxygène atomique sur Mars
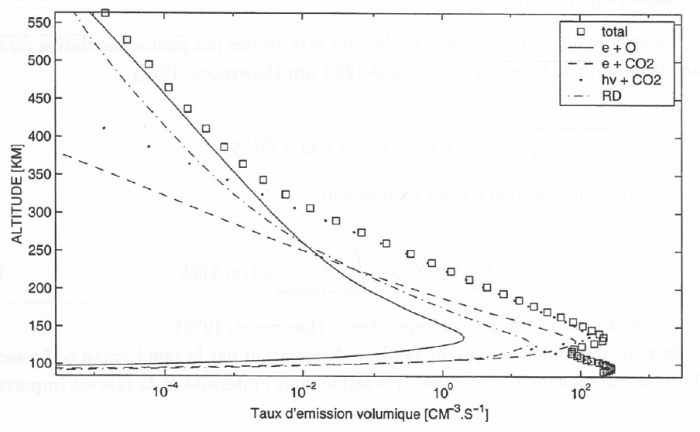
Modélisation des différents processus à l'origine de l'émission de l'oxygène à 297 nm
Crédit :
O. Witasse, (2000), Modélisation des ionosphères planétaires et de leur rayonnement : La Terre et Mars, thèse de doctorat
Ce modèle prédit que 75% de l'émission à 297 nm sur Mars est produite par l'excitation photodissociative de CO2. Il prédit aussi l'existence de deux pics d'émissivité. L'un vers 100 km et l'autre vers 150 km. Ces deux pics sont produits par la photodissociation excitative de CO2. Le pic au-dessous de 100 km est produit par les photons solaires de longueur d'onde 121.6 nm et le pic vers 150 km par les photons de longueurs d'onde entre 90 et 120 nm.
20% de l'émission est produite par l'excitation dissociative de CO2 par impact électronique. L'émission de l'oxygène à 297 nm est donc essentiellement un moyen d'étudier CO2 sur Mars. Cette émission dépend très peu de la densité de O et de O2+.
Emissions Aurorales: Généralités
Les émissions aurorales résultent de la précipitation de particules énergétiques « extra-atmosphériques » (le plus souvent des électrons) avec des énergies pouvant aller de quelques dizaines d’eV à plusieurs centaines de keV. Le terme « extra-atmosphérique » permet d’exclure les électrons produits par ionisation de l’atmosphère : les photoélectrons à l’origine de certaines émissions de l’airglow planétaire.
Les particules énergétiques sont produites par des mécanismes complexes liés à l’interaction du vent solaire avec la planète. Dans ce cours, nous ne verrons pas en détails les mécanismes d’accélération des électrons et les systèmes de courant responsables de ces précipitation. Nous verrons seulement l’effet de leur précipitation dans l’atmosphère des planètes.
Emissions aurorales terrestres
Sur Terre, la principale structure aurorale est une bande de forme ovale située aux hautes latitudes, centrée sur les pôles magnétiques. Il existe cependant de nombreuses autres structures moins brillantes que l’ovale auroral.
Les électrons excitent les espèces neutres atmosphériques qui en se désexcitant émettent un rayonnement appelé rayonnement auroral. La plupart des émissions décrites dans la section dayglow existent dans les émissions aurorales. Les émissions aurorales terrestres par exemple sont dominées par les raies d’émissions de l’oxygène et de l’azote. Dans le domaine visible, les émissions aurorales terrestres sont dominées par les raies rouge et verte de l’oxygène atomique décrites dans la section dayglow ainsi que les raies de N2 dans le violet – proche UV (300 – 380 nm). Dans l’UV plus lointain, on observe d’autres système de raies de N2 appelé Végard Kaplan (VK) (210 – 280 nm) et Lyman-Birge-Hopfield (LBH) (130 – 220 nm), ainsi que les raies déjà évoquées de l’oxygène atomique (297 nm, 135.6 nm, 130.4 nm) et de l’azote atomique (149.3 nm). Un exemple de spectre UV auroral terrestre obtenu par le satellite S3-4 est représenté sur la figure ci-dessous.
Exemple de spectre auroral observé en UV
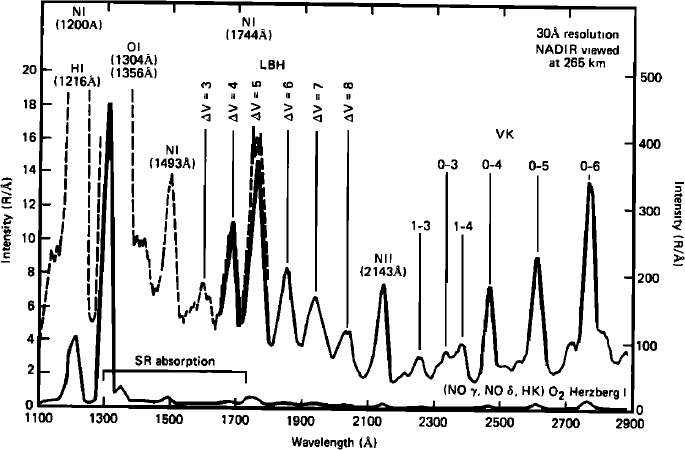
Spectre auroral composite obtenu par les spectromètres UV et VUV de la sonde S3-4
Crédit :
Ishimoto et al., J. Geophys. Res., 93, 9854, 1988
Emissions Aurorales des planètes géantes
Des aurores ont été observées sur plusieurs objets du système solaire, les plus intenses sont observées sur Terre, Jupiter et Saturne. Les sondes Voyager ont aussi observées des émissions aurorales UV sur Uranus et Neptune.
Des aurores très intenses ont été aussi observées dans les régions polaires de Jupiter et Saturne par le télescope Hubble. Sur Jupiter, on peut distinguer trois grand types de structures aurorales :
- un ovale auroral qui est la structure la plus brillante
- des points brillants provenant de l’interaction du plasma jovien avec les satellites ; le point le plus brillant sur la figure ci contre correpond à l’interaction Jupiter – Io.
- les aurores polaires qui se trouvent à des latitudes supérieures à l’oval auroral et dont la morphologie et l’intensité sont beaucoup plus variables
L’atmosphère de Jupiter et Saturne est essentiellement composée de H et H2. Les émissions aurorales UV observées sont donc essentiellement les émissions Lyman-α de l’hydrogène (121.6 nm) et les bandes électroniques Lyman et Werner de H2 (80 – 170 nm). Différents états vibrationnels de H2 peuvent être excités ce qui conduit non pas une raie d’émission unique mais à une série de raies appelées bandes.
Structure des émissions UV aurorales observées par le télescope Hubble
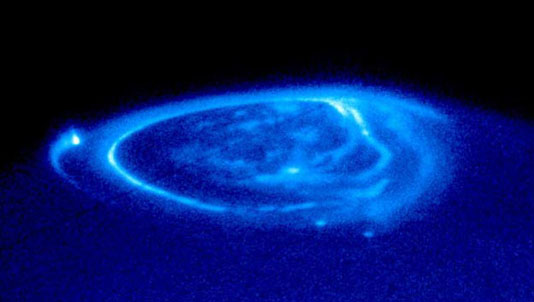
Emissions aurorales UV observées par le télescope Hubble
Crédit :
NASA and J. Clarke (University of Michigan)
Autres emissions aurorales dans le système solaire
Des émissions aurorales UV ont aussi été observées sur des objets non magnétisées. L’émission de l’oxygène à 130.4 nm a été observée la nuit sur Vénus et attribuée à des précipitation d’électrons dans l’atmosphère de Vénus. Sur Mars, la sonde Mars Express a observé des raies UV interdites la nuit, dont la source ne peut être que des électrons. Ces émissions sont liées au champ magnétique crustal des roches au voisinage de la surface de Mars.
Enfin pour compléter ce rapide survol des émissions aurorales UV sur les objets du système solaire, on peut ajouter que des aurores ont été observées sur d'autres objets, en particulier les satellites de Jupiter : Io, Ganymède et Europe. Sur Io, les principales signatures spectrales UV de ces aurores sont des raies d'émissions de l'oxygène atomique (130.4 ; 135.6 nm) et du soufre (147.9 et 190.0 nm). Sur Europe et Ganymède des raies d'oxygène produites principalement par excitation dissociatve de O2. Ganymède, le plus grand satellite de Jupiter est le seul satellite connu à posséder un champ magnétique intrinsèque. Ganymède est donc entouré de sa propre magnétosphère qui interagit avec le plasma magnétosphérique de Jupiter. La magnétosphère de Ganymède protège son atmosphère et sa surface aux basses latitudes. Les précipitations d'électrons et donc les aurores associées sont donc observées uniquement aux hautes latitudes là où les lignes de champ magnétique sont ouvertes et se reconnectent aux lignes de champ magnetique de Jupiter (cf figure ci dessous). L'intensité des émissions aurorales sur Ganymède est de quelques centaines de Rayleigh. On peut aussi noter sur la figure la présence d'une émission diffuse aux plus basses latitudes produites par l'impact des photoélectrons sur les espèces neutres de l'atmosphère de Ganymède.
Aurores UV sur Ganymède
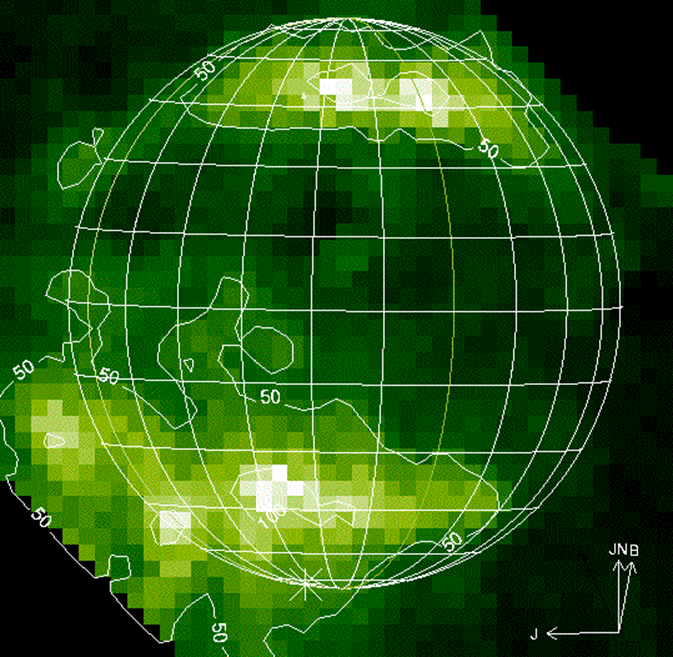
Emission de la raie d'oxygène à 135.6 nm sur Ganymède observée par le télescope Hubble
Crédit :
McGrath et al. (2013), J. Geophys. Res., 118, 2043
Emissions UV aurorales observées dans le système solaire
| Objets | Principales Espèces excitées |
| Terre | N2, O2, N, O, N2+, H |
| Jupiter | H2, H |
| Saturne | H2, H |
| Uranus | H2, H |
| Neptune | H2, H |
| Vénus | O, CO2 |
| Mars | O, CO2 |
| Io | O, S |
| Ganymède | O2 |
| Europe | O2 |
| Comètes | H2O, CO, CO2 |
Nightglow
Les processus d’excitation vus précédemment sont la plupart inopérants du côté nuit dû à l’absence de rayonnement solaire incident et de photoélectrons. Le principal mécanisme d’excitation est la recombinaison radiative. La recombinaison radiative entre deux atomes d’oxygène est à l’origine du système de bandes de Herzberg entre 250 et 390 nm observé sur Terre.
La recombinaison entre un atome d’oxygène et un atome d’azote est à l’origine du système de bandes γ et δ de NO (190 – 270 nm) observé sur Terre, Vénus et plus récemment sur Mars.
Ces atomes sont produits du côté jour par la dissociation des espèces moléculaires majeures (N2 et O2 sur Terre), (CO2 et N2 sur Mars et Vénus) et transportés côté nuit. Ces émissions sont donc des traceurs de la circulation atmosphérique à haute altitude (cf Exercice 2).
Le taux d’émissivité volumique est proportionnel à la densité des espèces atomiques qui se recombinent.
Du côté jour la densité de ces espèces est trop faible pour produire une émission importante comparée aux autres mécanismes vus précédemment.
Exercices
Auteur: Jean-Yves Chaufray
Exercice 1
 Séparation spectrale des raies Lyman-alpha de l'hydrogène et du deutérium
Séparation spectrale des raies Lyman-alpha de l'hydrogène et du deutérium
Difficulté : ☆☆☆
Temps : 30 minutes
Dans le modèle de Bohr présenté dans le cours, on a supposé que le proton était immobile, on suppose maintentant que le proton n’est pas immobile.
Question 1)
Montrer que le référentiel barycentrique du système est galiléen.
Question 3)
Réécrire l’équation de la dynamique pour l’électron et le proton dans le référentiel barycentrique et montrer que l'équation se réduit à la dynamique d'une particule de masse réduite μ que l'on exprimera en fonction de la masse de l'électron et du noyau.
Question 4)
On suppose que la trajectoire de cette particule réduite est circulaire, déterminer la vitesse angulaire de la particule réduite. On suppose que le moment cinétique de cette particule réduite est quantifié et ne peut prendre que des valeurs du type 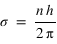 . déterminer les valeurs possibles de r et l'énergie de la particule en fonction de n.
. déterminer les valeurs possibles de r et l'énergie de la particule en fonction de n.
Question 5)
Calculer la longueur d’onde du photon émis lors de la transition du niveau m vers le niveau n de l’hydrogène et du deutérium atomique sachant que le noyau du deutérium est composé d'un proton et d'un neutron, on supposera que la masse d'un neutron est égale à la masse d'un proton.
Question 6)
La masse du proton est 1.672622x10-27 kg et la masse d'un électron de 9.109383x10-31 kg. En déduire la longueur d'onde des transitions Lyman-alpha de l'hydrogène et du deutérium et en deduire le pouvoir de résolution nécessaire pour séparer spectralement les deux raies.
Prendre des valeurs des constantes les plus précises possibles pour l'application numérique.
Exercice 2
 Détermination du flux d'azote descendant dans la nuit sur Mars
Détermination du flux d'azote descendant dans la nuit sur Mars
Difficulté : ☆
Temps : 10 minutes
Question 1)
L'émission UV de NO a été observée pour la première fois par la sonde Mars Express côté nuit sur Mars. L'intensité intégrée de la bande δ sur une colonne verticale entre 0 et 80 km a été estimée à 85 R. Cette émission est produite par la recombinaison des atomes O et N, produits côté jour à haute altitude et transporté à plus basse altitude côté nuit.
On suppose que 77% des recombinaisons produisent une émission dans la bande δ. On suppose que la perte d'azote par recombinaisons de N et O représentent 45% de la perte totale d'azote.
- On note L le taux de perte total d'atomes d'azote par unité de volume et par seconde. Déterminer le nombre de recombinaison LR entre N et O par unité de volume et par seconde.
- En déduire le nombre de recombinaison conduisant à une émission dans la bande δ de NO par unité de volume et par seconde. Ce terme est le taux d'émission volumique de la bande δ de NO
- Montrer que le taux de perte total de N intégré sur la colonne entre 0 et 80 km est proportionnel à l'intensité mesuré
- En déduire le flux d'azote nécessaire pour compenser cette perte (on convertira l'intensité en Rayleigh en ph/cm2/s)
Exercice 3 : Emission UV sur Europe
 Emission UV sur Europe
Emission UV sur Europe
Difficulté : ☆
Temps : 10 minutes
Question 1)
Sur Europe, des observations faites par le télescope Hubble en 1996 ont mis en évidence la présence des raies de l’oxygène à 130.4 nm et 135.6 nm
L’intensité mesurée de la raie à 130.4 nm est de 8.6 Rayleigh. L’intensité de la raie à 135.6 nm est de 12.9 Rayleigh.
Pourquoi cette observation indique qu’un mécanisme impliquant des électrons est forcément à l’origine d’une partie des émissions observées ?
Question 2)
Deux mécanismes ont été proposés pour expliquer ces émissions :
L’excitation de O par impact d’éléctrons (mécanisme 1)
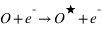
L’excitation dissociative par impact d’électrons de O2 (mécanisme 2)
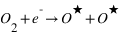
Exprimer le taux d’émission volumique à 130.4 et 135.6 nm pour chaque mécanisme en fonction de la densité de O et O2
Les valeurs des fréquences d’excitation à 130.4 et 135.6 nm de ces deux mécanismes sont données ci-dessous :
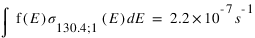
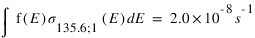
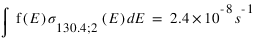
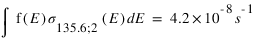
Quel mécanisme permet de mieux reproduire le rapport d'intensité observé ?
Mini Projet
Auteur: Jean-Yves Chaufray
Airglow
Dayglow
Les observations présentées ci-dessous ont été obtenues par la sonde Mars Express en regardant l'atmosphère en mode tangentielle (parallèle à l'horizon) pour étudier les émissions UV de la haute atmosphère de Mars.
http://exoplanetes.esep.pro/esep_outils/fluxuv/dayglow.html
Justifiez cette géométrie d'observation.
Regardez un spectre obtenu vers 120 km et un spectre observé à 200 km. Quelle différence observez vous ? A quelle espèce correspond la raie vers 121 nm ? Pourquoi reste t-elle visible à haute altitude ? La largeur de cette raie peut elle fournir des informations sur la température du milieu ?
Les bandes entre 180 nm et 260 nm sont des bandes interdites appelées bandes de Cameron correspondant à la transition électronique CO(a3Π) → CO(état fondamental). Sachant que CO2 est l’espèce majoritaire dans l’atmosphère de Mars au dessous de 180 km. Proposez un mécanisme d’excitation produisant ces émissions. Sur quelle autre planète du système solaire ces bandes devraient être importantes ? Pourquoi l’émission diminue au-dessous de 120 km ?
La raie à 289 nm est une raie de CO2+ produite par ionisation de CO2 par impact d'électron ou photoionization. Au dessus du pic d'intensité l’intensité devrait être proportionelle à la densité de CO2 à l’altitude du point tangent. Estimer la température à partir de cette émission. Est ce réaliste ?
Nightglow
On s’intéresse maintenant à d’autres observations mais obtenues du côté nuit.
http://exoplanetes.esep.pro/esep_outils/fluxuv/nightglow.html
Le spectre observé est t-il identique ou différent de celui observé du côté jour. Quel type de mécanisme peut être important du côté nuit ? Comment expliquer que la raie de l’hydrogène soit observée aussi du côté nuit ?
Comment expliquer l’augmentation de l’intensité de la raie Lyman-α quand on passe de 80 km à 130 km ?
Aurores planétaires
On va maintenant s’intéresser aux émissions aurorales planétaires observées par le télescope Hubble. Connectez vous sur le site APIS
https://apis.obspm.fr/
Cliquez sur login et connectez vous avec un compte temporaire.
Après connexion, lancez quelques recherches types : Regardez des observations HST de Jupiter, Saturne, Uranus et leurs lunes et ce qui les différencie. Que pensez-vous des observations de Mars ? Y voit-on des aurores. Quelle émission est observée sur Mars sur ces images ?
-------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------
ACCES AU PLAN DES CHAPITRES
Réponses aux exercices
pages_flux-uv/exercice1.html
Exercice
'Séparation spectrale des raies Lyman-alpha de l'hydrogène et du deutérium'
- Question 1
Solution :
L'équation de la dynamique de l'électron s'écrit:
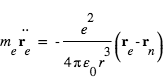
L'équation de la dynamique du noyau s'écrit:
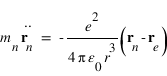
La somme de ces deux équations donne
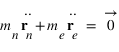
Par définition la position du barycentre du système est donnée par:
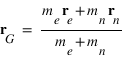
On en déduit que 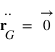
Le référentiel associé au barycentre est donc en mouvement uniforme par rapport au référentiel du laboratoire supposé galiléen. Le référentiel associé au barycentre est donc un référentiel galiléen.
- Question 2
Solution :
La position de l'électron dans le référentiel barycentrique est donnée par :
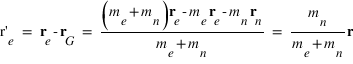
La position du noyau dans le référentiel barycentrique est donnée par :
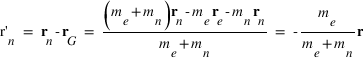
- Question 3
Solution :
Les équations de la dynamique de l'électron et du noyau dans le référentiel barycentrique s'écrivent:
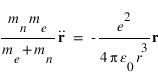
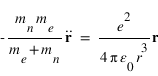
Il s'agit de deux fois la même équation de la dynamique d'une particule fictive de masse
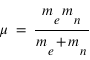 et de position
et de position 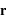
- Question 4
Solution :
La résolution de l'équation est identique à celle effectuée dans le cours en remplaçant me par μ. La force étant radiale, la trajectoire de la particule réduite est plane. En coordonnées cylindriques, les équations projetées sur les axes 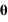 et
et 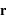 s'écrivent:
s'écrivent:
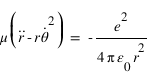
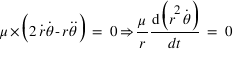
La deuxième équation conduit à
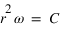
Comme on suppose que la trajectoire de la particule est circulaire
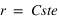
La première équation permet de déterminer la vitesse angulaire de la particule :
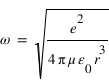
En utilisant la condition de quantification du moment cinétique, on obtient les valeurs de r et de l'énergie de la particule en fonction du nombre quantique n:
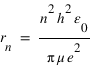
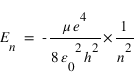
- Question 5
Solution :
En remplaçant μ par son expression avec mn = mp pour l'hydrogène et mn= 2mp pour le deutérium, on obtient:
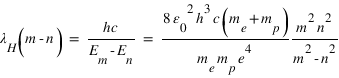
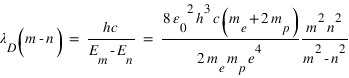
- Question 6
Aide :
Prendre des valeurs des constantes les plus précises possibles pour l'application numérique.
Solution :
L'émission Lyman-alpha correspond à la transition m = 2 vers n =1. L'application numérique donne λH = 121.568 nm et λD = 121.535 nm
Le pouvoir de résolution nécessaire pour séparer spectralement les deux raies est donc R = λ/dλ ≈ 3700.
pages_flux-uv/exercice2.html
Exercice
'Détermination du flux d'azote descendant dans la nuit sur Mars'
- Question 1
Solution :
Soit L le taux de perte total de N par unité de volume et par seconde. Le nombre de perte par recombinaison représente 45% des pertes totales donc LR = 0.45L
Le pourcentage de recombinaison conduisant à l'émission δ de NO est 77% donc le nombre de recombinaison produisant une émission dans la bande δ est 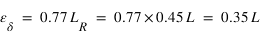
La perte d'azote sur la colonne verticale est
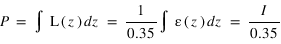
A l'équilibre, le flux d'azote incident Φ est égal à la perte P, en convertissant l'intensité en ph/cm2/s, on en déduit que le flux Φ = 2.5x108 cm-2.s-1
pages_flux-uv/exercice3.html
Exercice
'Emission UV sur Europe'
- Question 1
- Question 2
Solution :
L'émission de l'oxygène à 135.6 nm correspond à une raie interdite, elle ne peut donc pas être produite par les photons solaires. L'excitation par impact d'électron est le processus le plus probable pour expliquer cette raie
Les taux d'émissions volumiques sont données par
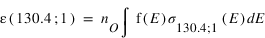
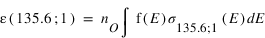
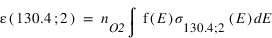
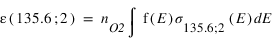
L'intensité s'obtient en intégrant le taux d'émission volumique sur la ligne de visée. Si l'on considère que les fréquences d'excitation sont des constantes, l'intensité est le produit entre cette fréquence et la colonne intégrée de O pour le mécanisme 1 et O2 pour le mécanisme 2. Le rapport des intensités pour le mécanismes 1 est donc :
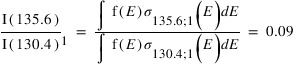
Le rapport des intensités pour le mécanisme 2 est :
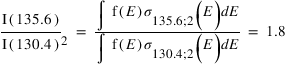
Le rapport mesuré vaut 1.5 ce qui est très proche de la valeur donnée par le deuxième mécanisme. L'émission observée est donc très probablement produite par l'excitation dissociative de O2. Cette observation permet donc d'étudier le dioxygène dans l'atmosphère de Europe.
 Prérequis
Prérequis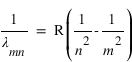 R est la constante de Rydberg, m et n sont deux nombres entiers. La structure en raies des spectres d'émission des atomes et la présence de nombre entiers dans l'équation de Rydberg suggère une quantification de l'énergie des électrons dans le nuage atomique, on parle de niveaux d'énergie. Les valeurs de l'énergie sont quantifiées par un nombre entier n et données par
R est la constante de Rydberg, m et n sont deux nombres entiers. La structure en raies des spectres d'émission des atomes et la présence de nombre entiers dans l'équation de Rydberg suggère une quantification de l'énergie des électrons dans le nuage atomique, on parle de niveaux d'énergie. Les valeurs de l'énergie sont quantifiées par un nombre entier n et données par
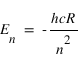 ou h est la constante de Planck et c la vitesse de la lumière dans le vide. Une raie d'émission résulte d'une transition d'un électron du niveau m vers le niveau n (m>n).
Cette quantification de l'énergie d'un atome ne peut s'expliquer par la physique classique. Bohr présentera un premier modèle théorique permettant de démontrer la formule de Rydberg-Ritz en 1913, mais c'est la physique quantique développée dans les années 1920 par Schrodinger et Heisenberg, puis la théorie des champs développée par Dirac qui permettront non seulement de retrouver la formule de Rydberg-Ritz mais aussi d'expliquer toutes les observations de la structure de l'hydrogène.
L'étude des émissions spectroscopiques est à la base de l'astrophysique.
ou h est la constante de Planck et c la vitesse de la lumière dans le vide. Une raie d'émission résulte d'une transition d'un électron du niveau m vers le niveau n (m>n).
Cette quantification de l'énergie d'un atome ne peut s'expliquer par la physique classique. Bohr présentera un premier modèle théorique permettant de démontrer la formule de Rydberg-Ritz en 1913, mais c'est la physique quantique développée dans les années 1920 par Schrodinger et Heisenberg, puis la théorie des champs développée par Dirac qui permettront non seulement de retrouver la formule de Rydberg-Ritz mais aussi d'expliquer toutes les observations de la structure de l'hydrogène.
L'étude des émissions spectroscopiques est à la base de l'astrophysique.
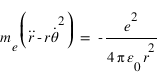
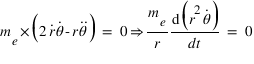
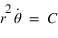 , comme la trajectoire est suppposée circulaire, la vitesse angulaire
, comme la trajectoire est suppposée circulaire, la vitesse angulaire 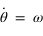 est constante.
Le moment cinétique est définit par
est constante.
Le moment cinétique est définit par 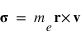 ou
ou 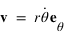 est le vecteur vitesse. Le moment cinétique est donc une constante donnée par
est le vecteur vitesse. Le moment cinétique est donc une constante donnée par
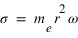 L'équation fondamentale de la dynamique projetée sur l'axe r qui traduit l'équilibre entre la force électrostatique et la force centrifuge peut se réécrire sous la forme:
L'équation fondamentale de la dynamique projetée sur l'axe r qui traduit l'équilibre entre la force électrostatique et la force centrifuge peut se réécrire sous la forme:
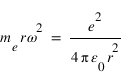 Ce qui permet de déterminer la vitesse angulaire
Ce qui permet de déterminer la vitesse angulaire 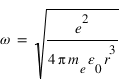
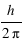 :
: 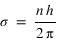 . On en déduit l'expression des rayons des orbites stationnaires :
. On en déduit l'expression des rayons des orbites stationnaires : 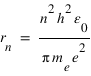 L'énergie totale de l'électron sur l'orbite quantifiée est la somme de son énergie potentielle électrostatique et de son énergie cinétique :
L'énergie totale de l'électron sur l'orbite quantifiée est la somme de son énergie potentielle électrostatique et de son énergie cinétique :
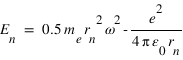 En remplaçant rn et
En remplaçant rn et 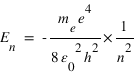
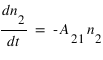
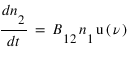
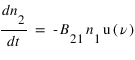
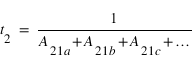
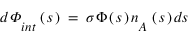

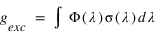
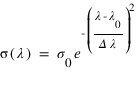
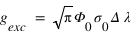
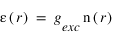
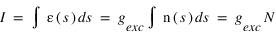
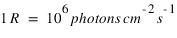



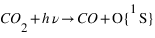
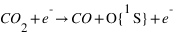
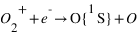
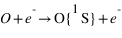
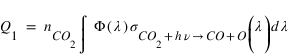
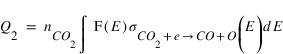
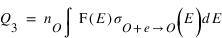
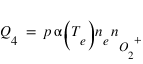
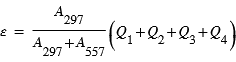




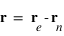 , où
, où 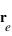 est la position de l'électron et
est la position de l'électron et 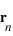 la position du noyau dans le référentiel du laboratoire, exprimer les positions de l'électron
la position du noyau dans le référentiel du laboratoire, exprimer les positions de l'électron 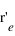 et du noyau
et du noyau 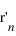 dans le référentiel barycentrique du système en fonction de
dans le référentiel barycentrique du système en fonction de 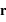
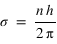 . déterminer les valeurs possibles de r et l'énergie de la particule en fonction de n.
. déterminer les valeurs possibles de r et l'énergie de la particule en fonction de n.
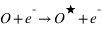
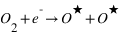
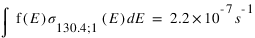
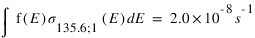
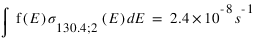
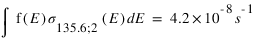
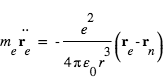
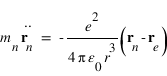
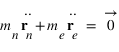
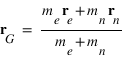
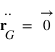
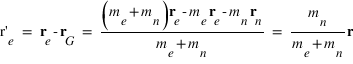
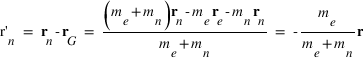
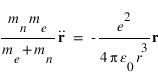
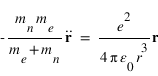
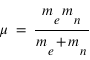 et de position
et de position 
 et
et  s'écrivent:
s'écrivent: