Occultations et transits : Page pour l'impression

La méthode des pelures d'oignon

L'observation d'une occultation au cours du lever (ou du coucher) de la source à travers l'atmosphère d'une planète permet d'inverser le profil vertical d'extinction 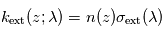$k_{\mathrm{ext}}(z;\lambda) = n(z) \sigma_{\mathrm{ext}}(\lambda)$ à la longueur d'onde 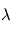$\lambda$ à partir de l'observation des transmissions 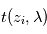$t(z_i,\lambda)$ selon différentes altitudes tangentes 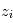z_i (altitude minimale du rayon lors de sa traversée de l'atmosphère). Un des algorithmes permettant cette inversion est appelé méthode des pelures d'oignon : on découpe l'atmosphère en coquilles sphériques concentriques homogènes à la manière d'un oignon. L'altitude tangente 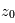z_0 la plus élevée pour laquelle on mesure 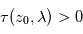$\tau(z_0,\lambda) > 0$ permet de déduire l'extinction locale 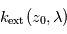$k_{\mathrm{ext}}(z_0,\lambda)$ au sein de cette couche la plus extérieure. La profondeur optique observée juste en-dessous, à l'altitude tangente 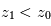z_1 < z_0 , est alors un peu plus grande. Comme on connaît déjà 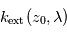$k_{\mathrm{ext}}(z_0,\lambda)$ , on en déduit 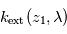$k_{\mathrm{ext}}(z_1,\lambda)$ pour la couche immédiatement intérieure. 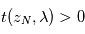Et ainsi de suite jusqu'au rayon le plus bas pour lequel on puisse mesurer une transmission $t(z_N,\lambda) > 0$ .

La mesure des profils d'extinction 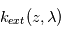$k_{\mathrrm{ext}}(z,\lambda)$ dans l'atmosphère permet alors d'en déduire plusieurs paramètres importants :

si on connaît la section efficace d'exinction 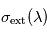$\sigma_{\mathrm{ext}}(\lambda)$ du constituant responsable de l'extinction, on peut en déduire sa densité locale 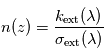$n(z) = \frac{k_{\mathrm{ext}}(\lambda)}{\sigma_{\mathrm{ext}}(\lambda)}$ . Si, en plus, le constituant responsable de l'extinction est bien mélangé, alors on sait que son profil vertical 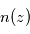suit la loi hydrostatique, c'est-à-dire une décroissance verticale localement exponentielle selon l'échelle de hauteur atmosphérique locale 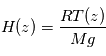$H(z) = \frac{RT(z)}{Mg}$ . La décroissance de 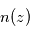avec l'altitude nous donne alors accès à 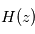et par conséquent au profil thermique 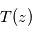au sein des couches sondées.
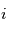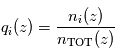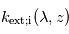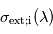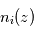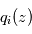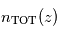pour une espèce dont le rapport de mélange $q_i(z) = \frac{n_i(z)}{n_{\mathrm{TOT}}(z)}$ n'est pas verticalement uniforme, la mesure de son profil d'extinction $k_{\mathrm{ext ; i}}(\lambda,z)$ et la connaissance de sa section efficace d'extinction $\sigma_{\mathrm{ext ; i}}(\lambda)$ permettent d'en déduire . On peut alors en déduire si $n_{\mathrm{TOT}}(z)$ est connu par ailleurs, par exemple grâce à la mesure du profil 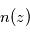d'un constituant bien mélangé et de rapport de mélange connu. 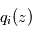est traditionnellement exprimé en ppmv (parties volumiques par million) pour des constituants mineurs, en pourcentage volumique sinon.
En dehors de l'extinction causée par les gaz, cette méthode donne aussi accès à l'extinction causée par les nuages et brumes (appelés collectivement aérosols) éventuellement présents dans l'atmosphère. Si les mesures des profils d'extinction sont faites à des longueurs d'onde assez éloignées les unes des autres, il est possible de remonter aux propriétés optiques des particules responsables de l'extinction car celles-ci varient habituellement de façon assez faible selon la longueur d'onde (contrairement par exemple aux gaz et leurs nombreuses raies spectrales). Une fois la section efficace d'extinction de ces particules ainsi contrainte, il est possible de déduire à partir des profils d'extinction mesurés le profil de densité volumique des aérosols au sein de l'atmosphère à condition de supposer ou d'avoir par ailleurs accès aux propriétés des diffuseurs individuels (forme, distribution statistique en taille, composition chimique ou au moins indices de réfraction).

Ces occultations sont donc une méthode précieuse de sondage atmosphérique, mais assez délicate à mettre en oeuvre. Il faut en effet pouvoir mesurer de nombreuses transmissions précisément, tout en connaissant parfaitement chacune des altitudes tangentes. Ceci n'est en général possible que pour un satellite en orbite autour de la planète, et nous restreint donc au système solaire.

Méthode dite "par pelure d'oignon"

Visualisation géométrique de la méthode d'inversion surnommée "par pelure d'oignon" : la transmission observée t(z_1)

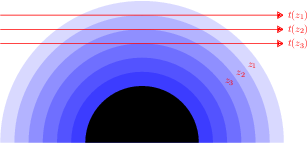
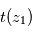permet, connaissant l'épaisseur traversée, de remonter à 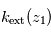$k_{\mathrm{ext}}(z_1)$ . À partir de là, la transmission t(z_2)

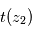permet, connaissant 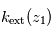$k_{\mathrm{ext}}(z_1)$ , d'en déduire 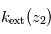$k_{\mathrm{ext}}(z_2)$ et ainsi de suite.

Crédit : Emmanuel Marcq CC-BY-SA

Transits primaires

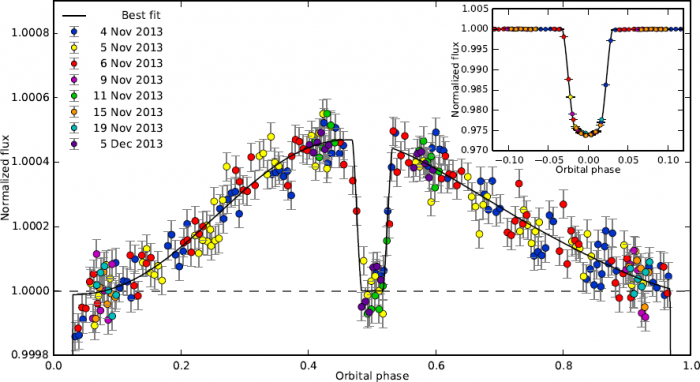
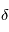L'observation d'un transit primaire se traduit par une baisse relative de luminosité en provenance de la source partiellement occultée, appelée profondeur du transit, notée $\delta$ et habituellement mesurée en ppm (parties par million). Pour une planète sans atmosphère, la profondeur est indépendante de la longueur d'onde (la réciproque n'est pas vraie : ainsi un plafond nuageux élevé peut conduire à la même observation, par exemple). En revanche, si l'atmosphère présente une extinction variable selon la longueur d'onde (que ce soit par absorption ou par diffusion Rayleigh par exemple), alors le rayon apparent de la planète (et donc la profondeur du transit) sembleront légèrement plus grands dans les longueurs d'onde où l'atmosphère cause davantage d'extinction.

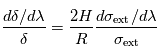On peut ainsi montrer, sous certaines hypothèses simplificatrices, que la variation relative de la profondeur du transit selon la longueur d'onde est liée à celle de la section efficace d'extinction (moyennée verticalement) au sein de l'atmosphère, selon la loi : $\frac{d \delta / d\lambda}{\delta} = \frac{2H}{R} \frac{d\sigma_{\mathrm{ext}} / d \lambda}{\sigma_{\mathrm{ext}}}$ où 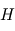désigne l'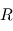échelle de hauteur de l'atmosphère et le rayon de la planète. Ces variations sont donc d'autant plus notables que l'échelle de hauteur est grande, ce qui favorise donc les atmosphères très dilatées. C'est par exemple le cas pour les Jupiter chauds (atmosphère légère constituée principalement de H₂ et à température élevée).

Spectroscopie d'un transit primaire

Visualisation de la profondeur d'un transit primaire en fonction de la longueur d'onde. Ici, l'atmosphère est transparente aux grandes longueurs d'onde, et de plus en plus opaque aux courtes longueurs d'onde, ce qui augmente la profondeur du transit.

Crédit : Emmanuel Marcq CC-BY-SA

Transits secondaires

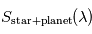L'intérêt d'un transit secondaire réside dans la possibilité d'effectuer une spectroscopie différentielle de la planète : si l'on mesure un spectre $S_{\mathrm{star + planet}}(\lambda)$ juste avant ou juste après ce transit secondaire, ainsi qu'un spectre 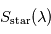$S_{\mathrm{star}}(\lambda)$ de l'étoile seule pendant ce transit secondaire, on peut en déduire le spectre 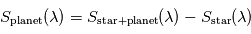$S_{\mathrm{planet}}(\lambda) = S_{\mathrm{star + planet}}(\lambda) - S_{\mathrm{star}}(\lambda)$ émis ou réfléchi par la planète seule vue à angle de phase nul.

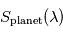Le spectre $S_{\mathrm{planet}}(\lambda)$ peut alors être analysé comme le serait n'importe quel spectre (par exemple en termes de température ou de composition pour un spectre thermique, ou bien de propriétés des diffuseurs pour un spectre réfléchi). C'est du moins le cas en théorie, car en pratique le faible rapport signal à bruit de tels spectres interdit à ce jour toute analyse trop poussée de ces spectres, de résolution spectrale souvent médiocre.

Courbe de lumière

Courbe de lumière lors du transit secondaire de WASP-43b. Le flux en provenance de l'étoile est normalisé à 1. Le surcroît autour du transit secondaire est causé par l'émission thermique de la planète, ce qui a permis de reconstituer son profil thermique. L'insert en haut à droite représente le transit primaire.

Crédit : Figure tirée de Stevenson et al. (2014)