Nadir : Page pour l'impression

Raies en absorption vs. émission

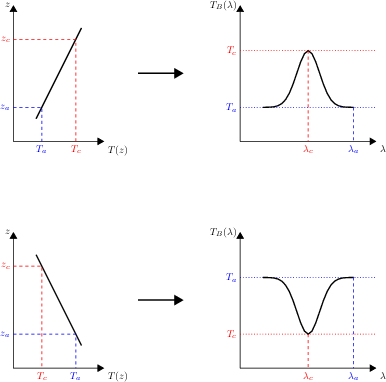
Nous sommes à présent en mesure d'interpréter pourquoi les raies caractéristiques de certains gaz apparaissent tantôt en absorption, tantôt en émission dans les spectres thermiques observés. En effet, le centre d'une raie spectrale présente une absorption massique plus grande que les ailes de cette même raie. En conséquence, du point de vue d'un observateur extérieur à l'atmosphère, la profondeur optique unité est atteinte à des altitudes plus élevées aux centres des raies que sur leurs ailes. À partir de là, on a les cas de figure suivants :

Lorsque le profil thermique décroît avec l'altitude (troposphère, mésosphère), les coeurs des raies atteint une profondeur optique de 1 à plus haute altitude, donc sondent un milieu de température plus faible que les ailes : les raies apparaissent alors en absorption.
Inversement, lorsque le profil thermique croît avec l'altitude (stratosphère), les coeurs des raies sondent un milieu de température plus élevée que les ailes : les raies apparaissent alors en émission.

Raies en absorption ou en émission

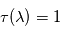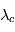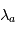Profils d'une raie spectrale vue en émission (haut) ou en absorption (bas). L'altitude $\tau(\lambda)=1$ est atteinte plus haut au coeur de la raie (longueur d'onde $\lambda_c$ ) que dans les ailes lointaines de la raie (longueur d'onde $\lambda_a$ ) : z_c < z_a

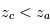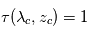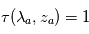avec $\tau(\lambda_c,z_c) = 1$ et $\tau(\lambda_a,z_a)=1$ .

Crédit : Emmanuel Marcq CC-BY-SA

Application

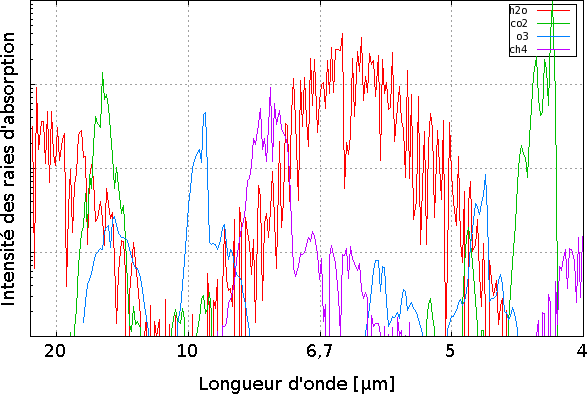
Lorsque le composé responsable d'une raie d'absorption est bien connu spectroscopiquement (son absorption en fonction de la longueur d'onde notamment) et que son profil d'abondance vertical est supposé connu au sein de l'atmosphère étudiée, il est possible de savoir à quelles altitudes sont atteintes les profondeurs optiques unité pour les différentes longueurs d'onde (ainsi, comme expliqué ci-dessus, le coeur des raies va sonder plus haut que les ailes lointaines des raies, où les rayons pourront même provenir de la surface si l'atmosphère est transparente par ailleurs). L'analyse du flux spectral reçu par l'observateur selon la longueur d'onde va alors lui permettre de reconstituer le profil thermique dans les plages d'altitudes associées aux différentes raies spectrales.

De façon semi-quantitative, lorsque la section efficace 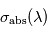$\sigma_{\mathrm{abs}}(\lambda)$ et le profil vertical en densité de l'absorbant 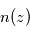n(z) sont connus, il est alors possible de trouver à quelle altitude 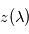$z(\lambda)$ on a $\tau \left[ z(\lambda) \right] = \int_{z(\lambda)}^{+\infty} \sigma_{\mathrm{abs}}(\lambda) n(z')\,dz' = 1$ . On sait alors qu'il règne une température $T\left[ z(\lambda) \right] \approx T_B(\lambda)$ à cette altitude. On a supposé dans ce calcul que la visée de l'observateur pointe verticalement vers le centre de la planète (visée nadir).

Sondages de composition

Principe

Lorsque le profil vertical de température est supposé connu dans une atmosphère planétaire (par exemple au moyen de la méthode décrite précédemment), il est possible d'utiliser les raies spectrales de composés identifiés (et bien connus spectroscopiquement) pour en déduire leur profil vertical d'abondance sur une plage d'altitudes donnée.

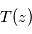De façon semi-quantitative et en visée nadir, on peut procéder comme suit : la connaissance du profil thermique T(z) permet, pour chaque longueur d'onde 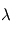$\lambda$ , de retrouver l'altitude 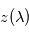$z(\lambda)$ correspondant à la température de brillance observée — en d'autres termes telle que $T_B(\lambda) = T\left[z(\lambda)\right]$ . 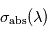Or, on sait que cette altitude correspond à la profondeur optique unité à la longueur d'onde considérée, si bien que l'on a $\tau \left[ z(\lambda) \right] = \sigma_{\mathrm{abs}}(\lambda) \times N\left[z(\lambda) \right] = 1$ où $\sigma_{\mathrm{abs}}(\lambda)$ désigne la section efficace d'absorption du composé mesuré (supposée ici indépendante de la pression et de la température) et 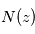N(z) la densité de colonne du composé recherché au-dessus de l'altitude 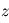, c'est-à-dire 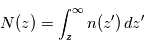$N(z) = \int_{z}^{\infty} n(z')\,dz'$ avec n(z') 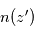la densité volumique de l'absorbant à l'altitude 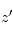. On peut alors en déduire par différentiation sur les altitudes sondées le profil de densité volumique 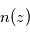n(z) du composé mesuré sur l'intervalle sondé.

Cependant, afin de moins dépendre des diverses approximations déjà évoquées, il est préférable d'utiliser un modèle de transfert de rayonnement afin de modéliser les spectres thermiques attendus et de les comparer ensuite aux observations en ajustant les différents paramètres (opération appelée fit en anglais de laboratoire). Notons que la procédure décrite ci-dessus ne fonctionne en pratique que lorsque les raies spectrales sont résolues, c'est-à-dire à une très haute résolution spectrale.

Il n'est en revanche pas possible d'inverser simultanément le profil thermique et le profil d'abondance du composé par la seule observation de ses raies d'absorption. On parle de problème dégénéré.

Absorption de quelques gaz dans l'IR thermique

Absorption de la vapeur d'eau (rouge), du dioxyde de carbone (vert), de l'ozone (bleu) et du méthane (violet) dans les conditions standard de température et de pression. L'échelle verticale est logarithmique.

Crédit : Emmanuel Marcq (à partir de la base de données GEISA 2011) CC-BY-SA

Spectre réfléchis

Réflectance

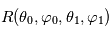La lumière stellaire réfléchie et reçue par un observateur extérieur a subi au moins un événement de diffusion, soit au sein de l'atmosphère (molécules de gaz, aérosols), soit par la surface pour une atmosphère peu opaque autour d'une planète tellurique. Ces propriétés de réflexion sont résumées par la fonction $R(\theta_0,\varphi_0,\theta_1,\varphi_1)$ appelée réflectance bidirectionnelle. C'est une fonction à quatre variables, deux pour caractériser la direction du rayon incident (d'angle zénital d'incidence 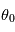$\theta_0$ et d'azimuth 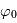$\varphi_0$ ) et deux pour celle du rayon émergent (d'angle d'émergence zénital 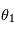$\theta_1$ et d'azimuth 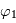$\varphi_1$ ) . C'est une fonction positive, dont la valeur minimale est nulle dans les directions où l'intensité réfléchie est nulle. Elle ne se déduit pas simplement des fonctions de phase calculables en régime de Rayleigh et de Mie, notamment à cause des phénomènes de diffusion multiple et de la possible contibution de la surface.

Transmission atmosphérique

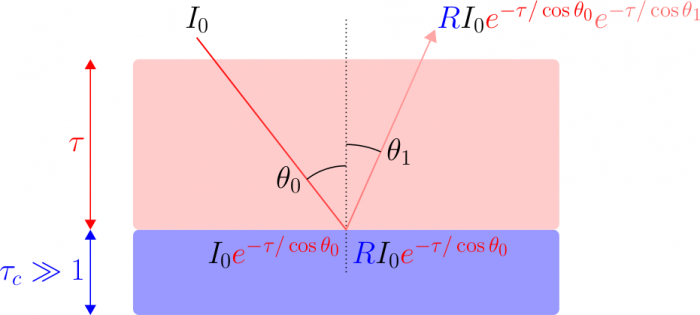
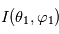Dans le cas d'une couche réfléchissante (surface, sommet des nuages) surmontée d'une atmosphère purement absorbante (non diffusante en elle-même), on a alors une relation anayltique entre l'intensité réfléchie $I(\theta_1,\varphi_1)$ et celle de la source 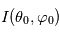$I(\theta_0,\varphi_0)$ : $I(\theta_1,\varphi_1) = I(\theta_0,\varphi_0) R(\theta_0,\varphi_0,\theta_1,\varphi_1) \exp \left[ - \tau \left(\frac{1}{\cos \theta_0} + \frac{1}{\cos \theta_1} \right) \right]$ où $\tau$ 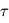désigne l'épaisseur optique de l'atmosphère au-dessus de la couche réfléchissante (comptée selon la verticale). Le terme en exponentielle provient de la loi de Beer-Lambert pour le rayon incident et le rayon émergent, en tenant compte de leur inclinaison éventuelle qui les amène à traverser des épaisseurs atmosphériques plus importantes que des rayons purement verticaux.

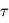Hormis l'étude la couche réfléchissante dans des longueurs d'onde où $\tau$ est négligeable, cette méthode permet de mesurer le spectre de l'absorption atmosphérique décrite par 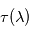$\tau(\lambda)$ : on a ainsi accès à la densité de colonne intégrée au-dessus de la couche réfléchissante en examinant la profondeur des raies d'absorption des composés atmosphériques. Notons qu'au contraire de l'émission thermique, la présence de composés absorbants se traduit toujours par des raies en absorption et non plus en émission.

Illustration de l'intensité réfléchie