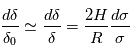 , d'où l'on tire
, d'où l'on tire 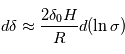 . La pente constante en
. La pente constante en 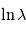 se traduit donc par
se traduit donc par 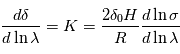 . Ceci n'est possible que si
. Ceci n'est possible que si 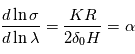 est constante, c'est-à-dire si
est constante, c'est-à-dire si 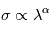 . Le phénomène le plus vraisembable est alors la diffusion Rayleigh causée par les molécules gazeuses. En ce cas,
. Le phénomène le plus vraisembable est alors la diffusion Rayleigh causée par les molécules gazeuses. En ce cas, 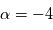 .
. 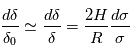 , d'où l'on tire
, d'où l'on tire 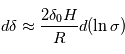 . La pente constante en
. La pente constante en 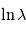 se traduit donc par
se traduit donc par 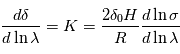 . Ceci n'est possible que si
. Ceci n'est possible que si 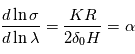 est constante, c'est-à-dire si
est constante, c'est-à-dire si 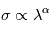 . Le phénomène le plus vraisembable est alors la diffusion Rayleigh causée par les molécules gazeuses. En ce cas,
. Le phénomène le plus vraisembable est alors la diffusion Rayleigh causée par les molécules gazeuses. En ce cas, 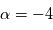 .
.