La planètes suivent les lois de la mécanique découvertes par Newton. En particulier, elles sont soumises à la force de gravitation universelle qui définit des orbites képlériennes.
La position et le mouvement relatif de la planète par rapport à son
étoile vont nous permettre de contraindre les éléments de l'orbite (demi
grand axe, inclinaison, excentricité), sa période et donc les masses des
corps.
Éléments d'une orbite
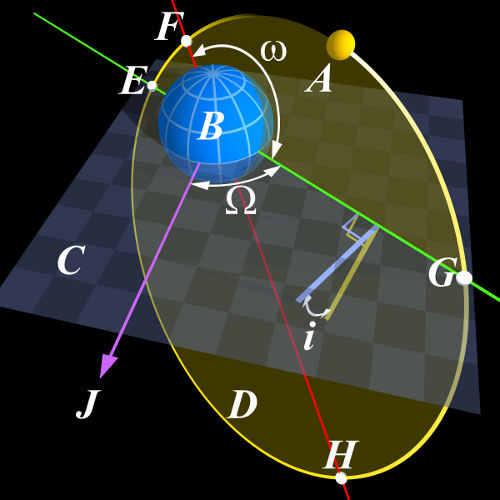
A – planète
B – étoile
C – plan de référence, l'écliptique
D – Plan orbital de la planète
E – noeud descendant
F – Périapse
G – noeud ascendant
H – Apoapse
i – Inclinaison
J – Direction de référence (ligne de visée)
Ω – Longitude du noeud ascendant
ω – Argument du périapse
Pour aller plus loin.
Une planète commence sa formation sous la forme d'un noyau solide qui grossit par accrétion de matière.
Si la masse de ce planétoïde dépasse quelques dizaines de 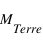 (1
(1 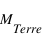 correspondant à une fois la masse Terre) , l'accrétion de gaz augmente brutalement pour former une planète géante.
correspondant à une fois la masse Terre) , l'accrétion de gaz augmente brutalement pour former une planète géante.
Naissance d'une planète géante
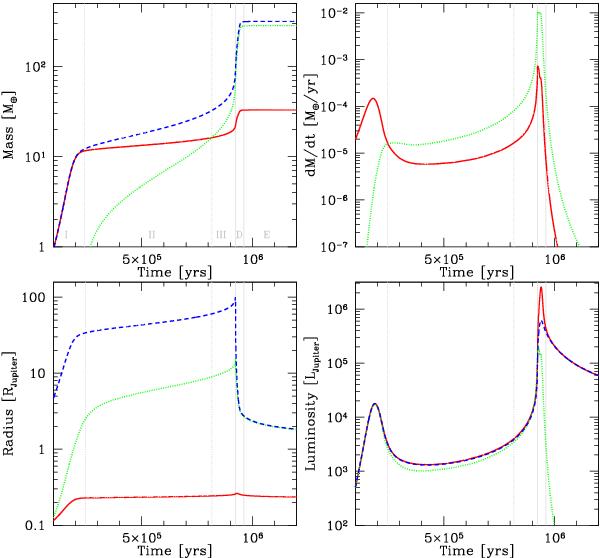
En 2012, Christoph Mordasini et collaborateurs publient dans Astronomy and Astrophysics une étude sur la formation des planètes, ici celle de Jupiter, de haut en bas et de gauche à droite, se trouvent l'évolution de la masse, du taux d'accrétion, du rayon et la luminosité de la planète en fonction du temps.
Remarque: Instabilités gravitationnelles
Le modèle précédent, dit de "core accretion" ou accrétion de coeur, n'est pas le seul existant pour expliquer la formation des planètes géantes, un autre modèle est basé sur les modèles de formation des étoiles. En effet les instabilités gravitationnelles dans le disque protoplanétaire provoquent une fragmentation de celui-ci suivi d'effondrements locaux menant à la formation directe d'astres principalement gazeux... Identifier le mode de formation est donc une tache complexe, et l'imagerie directe donne des pistes pour ce faire (notamment la luminosité ou la température en fonction de l'âge de la planète mais aussi sa position par rapport à l'étoile).
Pour en savoir plus, reportez-vous au cours sur la formation des planètes en cliquant ici.
Lorsqu'une étoile vient de se former, elle est entourée d'un disque de poussière et de gaz comme β Pictoris par exemple RAJOUTER LE LIEN. C'est dans ce dernier que vont se former les planètes.
Au fil de l'évolution du système planétaire, ce disque va être alimenté par les collisions entre les comètes et les astéroïdes. Ce disque de poussière est très lumineux dans les systèmes jeunes. Il absorbe le rayonnement de l'étoile et son émission (principalement dans l'infrarouge lointain) va avoir tendance à gêner l'observation directe des exoplanètes.
Dans le système solaire le contraste moyen entre la lumière zodiacale et la lumière solaire est de 7 ordres de grandeur.
alors que le rapport des masses entre le disque de poussière et les planètes vaut 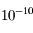 et que le disque s'étend de 5 à plusieurs centaines d'UA.
Il existe des étoiles autour desquelles on trouve un disque plus de 1200 fois plus brillant, comme η Corvi !
et que le disque s'étend de 5 à plusieurs centaines d'UA.
Il existe des étoiles autour desquelles on trouve un disque plus de 1200 fois plus brillant, comme η Corvi !
On exprime l'intensité diffusée par la poussière interplanétaire en zodi, 1 zodi étant l'intensité diffusée par le disque de notre système solaire.
Disque

Image composite combinant le disque et la planète en orbite autour de β pictoris (ici masquée, au centre du cercle) .
Tout corps, à une température donnée, émet un rayonnement particulier appelé rayonnement thermique (ou par abus, rayonnement de corps noir, un corps noir étant un corps parfaitement absorbant à toutes les longueurs d'onde).
Le spectre du rayonnement d'un corps noir ne dépend que de sa température 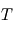 . La longueur d'onde
. La longueur d'onde 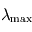 où ce spectre atteint son maximum est donnée par la loi de Wien:
où ce spectre atteint son maximum est donnée par la loi de Wien: 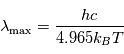 .
. 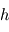 ,
, 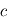 et
et 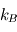 désignent respectivement les constantes de Planck, la vitesse de la lumière et la constante de Boltzmann. Un corps chaud présente donc un pic d'émission décalé vers les courtes longueurs d'onde par rapport à un corps plus froid. Aux températures ambiantes, ce pic est dans l'infrarouge (dit infrarouge thermique), mais pour des corps atteignant une température plusieurs milliers de Kelvins, ce maximum se décale dans le spectre visible : c'est le cas des étoiles par exemple, ou bien d'un tison chauffé à blanc.
désignent respectivement les constantes de Planck, la vitesse de la lumière et la constante de Boltzmann. Un corps chaud présente donc un pic d'émission décalé vers les courtes longueurs d'onde par rapport à un corps plus froid. Aux températures ambiantes, ce pic est dans l'infrarouge (dit infrarouge thermique), mais pour des corps atteignant une température plusieurs milliers de Kelvins, ce maximum se décale dans le spectre visible : c'est le cas des étoiles par exemple, ou bien d'un tison chauffé à blanc.
Le flux total 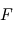 (intégré sur toutes les longueurs d'onde) émis par un corps noir ne dépend également que de sa température, suivant la loi de Stefan-Boltzmann :
(intégré sur toutes les longueurs d'onde) émis par un corps noir ne dépend également que de sa température, suivant la loi de Stefan-Boltzmann : 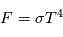 où
où 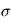 désigne la constante de Stefan-Boltzmann. Un corps chaud rayonne donc bien davantage qu'un corps froid.
désigne la constante de Stefan-Boltzmann. Un corps chaud rayonne donc bien davantage qu'un corps froid.
La température du corps noir émettant autant de flux thermique que la planète est appelée température efficace (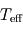 ) de la planète. Elle est en règle générale voisine de la température physique de la région de la planète d'où est principalement issue l'émission thermique (atmosphère, voire surface solide pour des planètes telluriques dotées d'une atmosphère mince).
) de la planète. Elle est en règle générale voisine de la température physique de la région de la planète d'où est principalement issue l'émission thermique (atmosphère, voire surface solide pour des planètes telluriques dotées d'une atmosphère mince).
Or, on a pu voir précédemment, que le processus de formation des planètes était un processus impliquant des chocs et autres phénomènes violents, ce qui provoque un dégagement d'énergie considérable sous forme de chaleur.
Evolution température
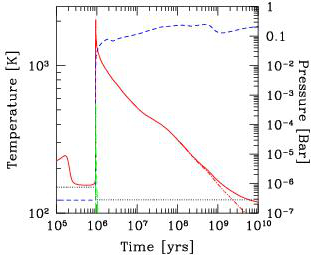
En 2012, Christoph Mordasini et collaborateurs publient dans Astronomy & Astrophysics une étude sur la formation des planètes, ici celle de Jupiter. En rouge vous pouvez remarquer l'évolution de la température efficace de la planète en fonction du temps.
Vous pouvez remarquer que, une fois formée, plus la planète est jeune, plus elle est chaude, et donc plus important est le flux lumineux qu'elle émet. Mais aussi plus la longueur d'onde du maximum de luminosité est courte (et se rapproche du domaine visible) ! Ainsi Jupiter émet actuellement son maximum d'émission autour de 30 µm, tandis que β Pictoris b l'émet autour de 1,7 µm.
Pour en savoir plus.
Le rayonnement de corps noir des jeunes exoplanètes géantes culmine généralement dans le proche infrarouge. C'est une chance car il y a de nombreuses raies moléculaires (méthane, monoxyde de carbone...) et atomiques (Na, K ...) dans ce domaine spectral, ce qui permet potentiellement d'analyser la composition chimique de ces planètes.
Pour observer depuis le sol dans ce domaine de longueurs d'onde, il faut hélas se restreindre aux fenêtres de transparence de l'atmosphère terrestre, comme les fenêtres J,H et K situées dans le proche infrarouge (voir l'image ci-dessous).
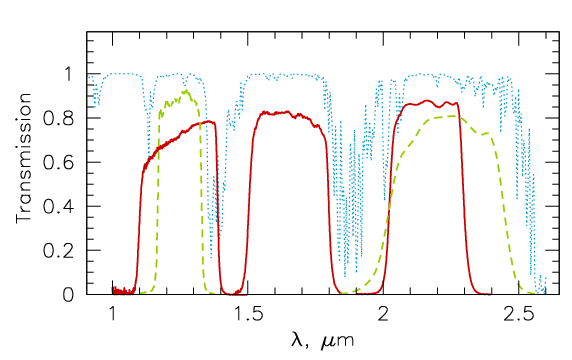
Filtres J (∼1,1-1,4 μm), H(∼1,5-1,8 μm) et (∼2-2,5 μm)K (en rouge et vert) disponible dans le proche infrarouge à l'ESO, comparé à la transmission de l'atmosphère terrestre (bleu).
La formation des planètes étant quasi-concomittante à celle de leur étoile hôte, on assimile souvent l'âge de la planète à celui de son étoile. Par exemple la Terre a terminé sa formation 20 millions d'années après le Soleil, ce qui est négligeable en comparaison des 4,6 milliards d'années du système solaire.
Fragmentation d'un nuage interstellaire
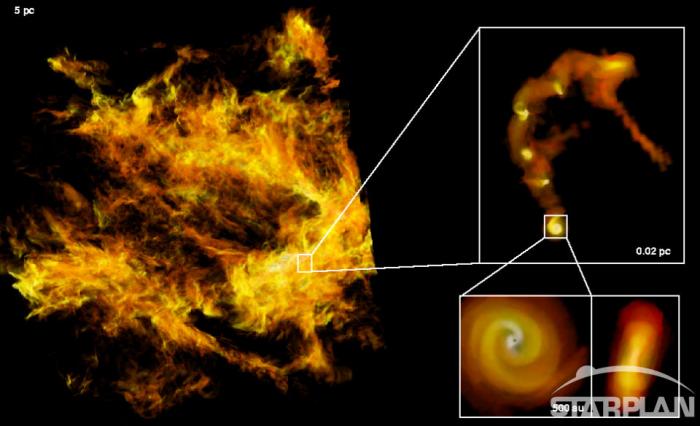
Modèle de formation de disque protoplanétaire par fragmentations d'un nuage se situant dans le milieu interstellaire. Dans ce nuage un très grand nombre d'étoiles sont en formation en même temps, mais elles sont de masses différentes. Nous allons pouvoir répartir les étoiles résultantes sur un diagramme HR et, suivant leur emplacement, pouvoir dater le groupe d'étoiles et donc contraindre l'âge des exoplanètes possiblement présentes.
Groupe local
Pour déterminer l'âge d'une étoile on peut déterminer, par son mouvement propre, à quel groupe d'étoiles elle appartient. Le groupe d'étoiles, dont les étoiles ont été formées au même moment et se déplaçant dans la même direction, peut nous donner son âge grâce à sa répartition au sein du diagramme HR.
http://astro.unl.edu/naap/hr/animations/hr.html
Activité
Age/Activité
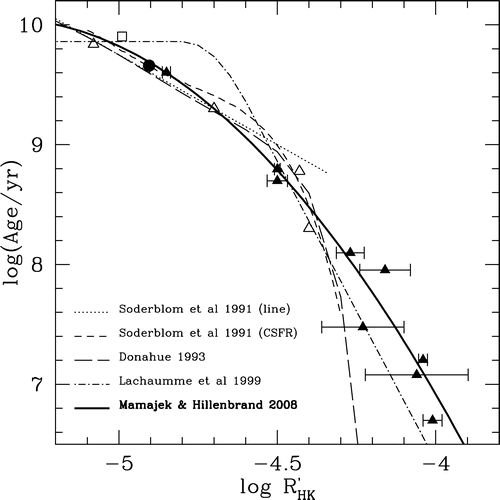
Eric E. Mamajek et Lynne A. Hillenbrand ont publié en 2008 dans
the Astrophysical Journal une étude sur les estimateurs d'âge des étoiles de type solaire. Ce graphique nous présente la répartition des âges, en ordonnées (en années et en échelle logarithmique), en fonction d'un marqueur d'activité à savoir
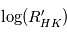
: plus il est élevé, plus l'activité est grande. Les courbes représentes plusieurs tentatives pour déterminer une relation entre ces deux observables.
On peut aussi relier, pour un type stellaire donné, l'âge à l'activité et à la couleur de l'étoile. La couleur s'obtient en prenant deux mesures de flux photométriques dans deux domaines de longueur d'onde différents. Pour l'activité, l'observation de plusieurs marqueurs spectroscopiques est possible ainsi que l'émission dans le domaine des rayons X.
Activité/X
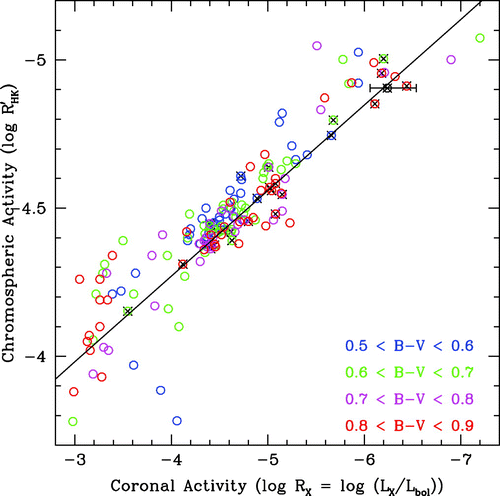
Dans le même article de Eric E. Mamajek et Lynne A. Hillenbrand, on trouve ce graphique qui nous présente une relation linéaire entre le marqueur spectroscopique qu'est le
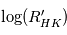
et le rayonnement en X .
B-V est l'indice de couleur des étoiles qui peut donc être relié à leur type spectral.
Rotation
La rotation de l'étoile est aussi liée à l'activité et donc à son âge, la comparaison de la rotation propre d'une étoile avec sa couleur va donc nous permettre de remonter à ce premier paramètre, pour un type spectral donné.
Rotation/Activité
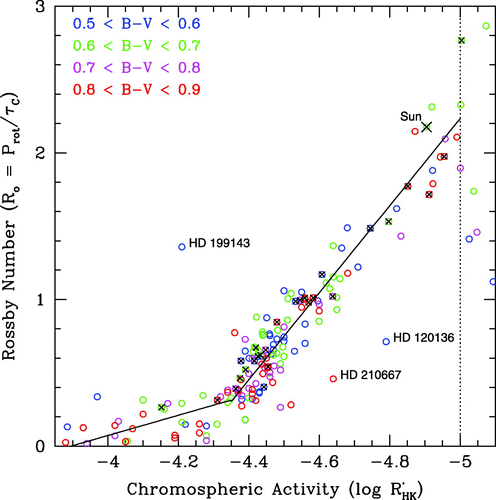
L'article de Eric E. Mamajek et Lynne A. Hillenbrand présente enfin ce graphique qui nous présente les relations linéaires entre le marqueur spectroscopique qu'est le
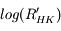
et la rotation de l'étoile exprimée par le
nombre de Rossby.


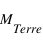 (1
(1 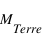 correspondant à une fois la masse Terre) , l'accrétion de gaz augmente brutalement pour former une planète géante.
correspondant à une fois la masse Terre) , l'accrétion de gaz augmente brutalement pour former une planète géante.

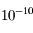 et que le disque s'étend de 5 à plusieurs centaines d'UA.
Il existe des étoiles autour desquelles on trouve un disque plus de 1200 fois plus brillant, comme η Corvi !
et que le disque s'étend de 5 à plusieurs centaines d'UA.
Il existe des étoiles autour desquelles on trouve un disque plus de 1200 fois plus brillant, comme η Corvi !

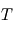 . La longueur d'onde
. La longueur d'onde 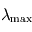 où ce spectre atteint son maximum est donnée par la loi de Wien:
où ce spectre atteint son maximum est donnée par la loi de Wien: 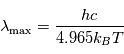 .
. 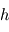 ,
, 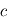 et
et 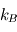 désignent respectivement les constantes de Planck, la vitesse de la lumière et la constante de Boltzmann. Un corps chaud présente donc un pic d'émission décalé vers les courtes longueurs d'onde par rapport à un corps plus froid. Aux températures ambiantes, ce pic est dans l'infrarouge (dit infrarouge thermique), mais pour des corps atteignant une température plusieurs milliers de Kelvins, ce maximum se décale dans le spectre visible : c'est le cas des étoiles par exemple, ou bien d'un tison chauffé à blanc.
désignent respectivement les constantes de Planck, la vitesse de la lumière et la constante de Boltzmann. Un corps chaud présente donc un pic d'émission décalé vers les courtes longueurs d'onde par rapport à un corps plus froid. Aux températures ambiantes, ce pic est dans l'infrarouge (dit infrarouge thermique), mais pour des corps atteignant une température plusieurs milliers de Kelvins, ce maximum se décale dans le spectre visible : c'est le cas des étoiles par exemple, ou bien d'un tison chauffé à blanc.
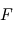 (intégré sur toutes les longueurs d'onde) émis par un corps noir ne dépend également que de sa température, suivant la loi de Stefan-Boltzmann :
(intégré sur toutes les longueurs d'onde) émis par un corps noir ne dépend également que de sa température, suivant la loi de Stefan-Boltzmann : 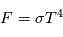 où
où 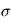 désigne la constante de Stefan-Boltzmann. Un corps chaud rayonne donc bien davantage qu'un corps froid.
désigne la constante de Stefan-Boltzmann. Un corps chaud rayonne donc bien davantage qu'un corps froid.
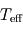 ) de la planète. Elle est en règle générale voisine de la température physique de la région de la planète d'où est principalement issue l'émission thermique (atmosphère, voire surface solide pour des planètes telluriques dotées d'une atmosphère mince).
) de la planète. Elle est en règle générale voisine de la température physique de la région de la planète d'où est principalement issue l'émission thermique (atmosphère, voire surface solide pour des planètes telluriques dotées d'une atmosphère mince).




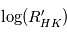 : plus il est élevé, plus l'activité est grande. Les courbes représentes plusieurs tentatives pour déterminer une relation entre ces deux observables.
: plus il est élevé, plus l'activité est grande. Les courbes représentes plusieurs tentatives pour déterminer une relation entre ces deux observables.

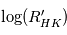 et le rayonnement en X .
B-V est l'indice de couleur des étoiles qui peut donc être relié à leur type spectral.
et le rayonnement en X .
B-V est l'indice de couleur des étoiles qui peut donc être relié à leur type spectral.

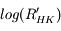 et la rotation de l'étoile exprimée par le
et la rotation de l'étoile exprimée par le