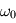 , de la forme
, de la forme 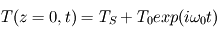 .
La solution s'écrit
.
La solution s'écrit 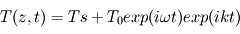 .
Par identification, on a donc
.
Par identification, on a donc 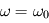 .
.
On considère un forçage en surface correpondant à une pulsation 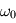 , de la forme
, de la forme 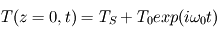 .
La solution s'écrit
.
La solution s'écrit 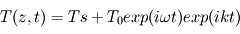 .
Par identification, on a donc
.
Par identification, on a donc 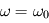 .
.
En appliquant l'équation de diffusion de la chaleur, on obtient la relation 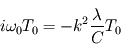 .
D'où les deux solutions
.
D'où les deux solutions 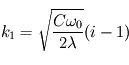 et
et 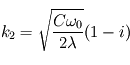
La solution avec 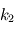 n'est pas physique, car elle donne une augmentation exponentielle du champ
n'est pas physique, car elle donne une augmentation exponentielle du champ 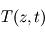 lorsque
lorsque 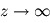 .
La solution finale s'écrit
.
La solution finale s'écrit 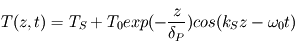 avec une fréquence spatiale
avec une fréquence spatiale 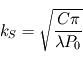 , une épaisseur de peau
, une épaisseur de peau 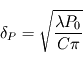 , et
, et 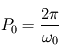
On se fixe comme critère que la profondeur minimale 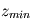 du sous-sol doit être telle qu'on représente le champ de température pour toutes les ondes :
du sous-sol doit être telle qu'on représente le champ de température pour toutes les ondes : 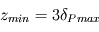 A priori, la période la plus élevée est la période annuelle (les cycles pluriannuels, plus subtiles, ne font pas partie de cette étude) :
A priori, la période la plus élevée est la période annuelle (les cycles pluriannuels, plus subtiles, ne font pas partie de cette étude) : 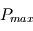 vaut 150 jours.
L'application numérique donne une profondeur minimale de 6,7 mètres.
vaut 150 jours.
L'application numérique donne une profondeur minimale de 6,7 mètres.